
【题目】设函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的零点个数;
的零点个数;
(2)若![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2) ![]()
【解析】
(1)利用![]() 的符号讨论函数的单调性,结合零点存在定理可得零点的个数.
的符号讨论函数的单调性,结合零点存在定理可得零点的个数.
(2)不等式有解等价于![]() 对任意
对任意![]() 恒成立即
恒成立即![]() ,构建新函数
,构建新函数![]() ,求出
,求出![]() 后分
后分![]() 和
和![]() 分类讨论可得实数
分类讨论可得实数![]() 的取值范围.
的取值范围.
解:(1)![]() ,即
,即![]() ,
,
则![]() ,
,
令![]() 解得
解得![]() .
.
当![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 在
在![]() 上单调递增,
上单调递增,
所以当![]() 时,
时,![]() .
.
因为![]() ,
,
所以![]() .
.
又![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() 分别在区间
分别在区间![]() 上各存在一个零点,函数
上各存在一个零点,函数![]() 存在两个零点.
存在两个零点.
(2)假设![]() 对任意
对任意![]() 恒成立,
恒成立,
即![]() 对任意
对任意![]() 恒成立.
恒成立.
令![]() ,则
,则![]() .
.
①当![]() ,即
,即![]() 时,且
时,且![]() 不恒为0,
不恒为0,
所以函数![]() 在区间
在区间![]() 上单调递增.
上单调递增.
又![]() ,所以
,所以![]() 对任意
对任意![]() 恒成立.
恒成立.
故![]() 不符合题意;
不符合题意;
②当![]() 时,令
时,令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]() .
.
所以函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
所以![]() ,即当
,即当![]() 时,存在
时,存在![]() ,使
,使![]() ,即
,即![]() .
.
故![]() 符合题意.
符合题意.
综上可知,实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】近年来,随着互联网的发展,诸如“滴滴打车”“神州专车”等网约车服务在我国各城市迅猛发展,为人们出行提供了便利,但也给城市交通管理带来了一些困难.为掌握网约车在![]() 省的发展情况,
省的发展情况,![]() 省某调查机构从该省抽取了5个城市,分别收集和分析了网约车的
省某调查机构从该省抽取了5个城市,分别收集和分析了网约车的![]() ,
,![]() 两项指标数
两项指标数![]() ,数据如下表所示:
,数据如下表所示:
城市1 | 城市2 | 城市3 | 城市4 | 城市5 | |
| 2 | 4 | 5 | 6 | 8 |
| 3 | 4 | 4 | 4 | 5 |
经计算得: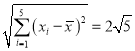 ,
,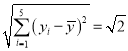 ,
,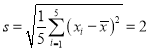 .
.
(1)试求![]() 与
与![]() 间的相关系数
间的相关系数![]() ,并利用
,并利用![]() 说明
说明![]() 与
与![]() 是否具有较强的线性相关关系(若
是否具有较强的线性相关关系(若![]() ,则线性相关程度很高,可用线性回归模型拟合);
,则线性相关程度很高,可用线性回归模型拟合);
(2)建立![]() 关于
关于![]() 的回归方程,并预测当
的回归方程,并预测当![]() 指标数为7时,
指标数为7时,![]() 指标数的估计值;
指标数的估计值;
(3)若城市的网约车![]() 指标数
指标数![]() 落在区间
落在区间![]() 之外,则认为该城市网约车数量过多,会对城市交通管理带来较大的影响,交通管理部门将介入进行治理,直至
之外,则认为该城市网约车数量过多,会对城市交通管理带来较大的影响,交通管理部门将介入进行治理,直至![]() 指标数
指标数![]() 回落到区间
回落到区间![]() 之内.现已知2018年11月该城市网约车的
之内.现已知2018年11月该城市网约车的![]() 指标数为13,问:该城市的交通管理部门是否要介入进行治理?试说明理由.
指标数为13,问:该城市的交通管理部门是否要介入进行治理?试说明理由.
附:相关公式: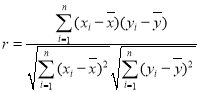 ,
,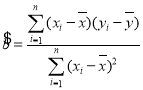 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,底面
中,底面![]() 是正方形,顶点
是正方形,顶点![]() 在底面的射影是底面的中心,且各顶点都在同一球面上,若该四棱锥的侧棱长为
在底面的射影是底面的中心,且各顶点都在同一球面上,若该四棱锥的侧棱长为![]() ,体积为4,且四棱锥的高为整数,则此球的半径等于( )(参考公式:
,体积为4,且四棱锥的高为整数,则此球的半径等于( )(参考公式:![]() )
)
A. 2B. ![]() C. 4D.
C. 4D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,以原点
中,以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,两种坐标系中取相同的长度单位.已知圆
轴的正半轴为极轴建立极坐标系,两种坐标系中取相同的长度单位.已知圆![]() 是以极坐标系中的点
是以极坐标系中的点![]() 为圆心,
为圆心,![]() 为半径的圆,直线
为半径的圆,直线![]() 的参数方程为
的参数方程为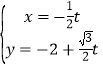 .
.
(1)求![]() 与
与![]() 的直角坐标系方程;
的直角坐标系方程;
(2)若直线![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,圆
,圆![]() 经过椭圆
经过椭圆![]() 的两个焦点和两个顶点,点
的两个焦点和两个顶点,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() ,
,![]() .
.
(Ⅰ)求椭圆![]() 的方程和点
的方程和点![]() 的坐标;
的坐标;
(Ⅱ)过点![]() 的直线
的直线![]() 与圆
与圆![]() 相交于
相交于![]() 、
、![]() 两点,过点
两点,过点![]() 与
与![]() 垂直的直线
垂直的直线![]() 与椭圆
与椭圆![]() 相交于另一点
相交于另一点![]() ,求
,求![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果函数![]() 在定义域内存在区间[a,b],使
在定义域内存在区间[a,b],使![]() 在[a,b]上的值域是[2a,2b],那么称
在[a,b]上的值域是[2a,2b],那么称![]() 为“倍增函数”。
为“倍增函数”。
(I)判断![]() =
=![]() 是否为“倍增函数”,并说明理由;
是否为“倍增函数”,并说明理由;
(II)证明:函数![]() =
=![]() 是“倍增函数”;
是“倍增函数”;
(III)若函数![]() =ln(
=ln(![]() )是“倍增函数”,写出实数m的取值范围。(只需写出结论)
)是“倍增函数”,写出实数m的取值范围。(只需写出结论)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com