
ЁОЬтФПЁПдк2018Фъ3дТжЃжнЕкЖўДЮФЃФтПМЪджаЃЌФГаЃЙВга100УћЮФПЦбЇЩњВЮМгПМЪдЃЌЦфжагяЮФПМЪдГЩМЈЕЭгк130ЕФеМ95%ШЫЃЌЪ§бЇГЩМЈЕФЦЕТЪЗжВМжБЗНЭМШчЭМЃК
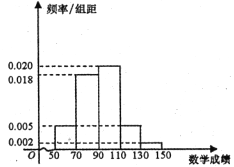
ЃЈЂёЃЉШчЙћГЩМЈВЛЕЭгк130ЕФЮЊЬиБ№гХауЃЌет100УћбЇЩњжаБОДЮПМЪдгяЮФЁЂЪ§бЇГЩМЈЬиБ№гХауЕФДѓдМИїЖрЩйШЫЃП
ЃЈЂђЃЉШчЙћгяЮФКЭЪ§бЇСНПЦЖМЬиБ№гХауЕФЙВга3ШЫЃЎ
ЃЈЂЁЃЉДгЃЈЂёЃЉжаЕФетаЉЭЌбЇжаЫцЛњГщШЁ2ШЫЃЌЧѓетСНШЫСНПЦГЩМЈЖМгХауЕФИХТЪЃЎ
ЃЈЂЂЃЉИљОнвдЩЯЪ§ОнЃЌЭъГЩ![]() СаСЊБэЃЌВЂЗжЮіЪЧЗёга99%ЕФАбЮеШЯЮЊгяЮФЬиБ№гХауЕФЭЌбЇЃЌЪ§бЇвВЬиБ№гХауЃЎ
СаСЊБэЃЌВЂЗжЮіЪЧЗёга99%ЕФАбЮеШЯЮЊгяЮФЬиБ№гХауЕФЭЌбЇЃЌЪ§бЇвВЬиБ№гХауЃЎ
гяЮФЬиБ№гХау | гяЮФВЛЬиБ№гХау | КЯМЦ | |
Ъ§бЇЬиБ№гХау | |||
Ъ§бЇВЛЬиБ№гХау | |||
КЯМЦ |
![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
ЁОД№АИЁПЃЈЂёЃЉ![]() ЃЛЃЈЂђЃЉ(i)
ЃЛЃЈЂђЃЉ(i)![]() ЃЌЃЈiiЃЉгаАбЮе.
ЃЌЃЈiiЃЉгаАбЮе.
ЁОНтЮіЁПЗжЮіЃКЃЈ1ЃЉгЩЦЕТЪЗжВМжБЗНЭМЧѓГіГЩМЈВЛЕЭгк130ЕФИХТЪЃЌНјЖјЕУЕНЧѓНтЃЌ
ЃЈ2ЃЉСаОйГіЫљгаЛљБОЪТМўЃЌ
ЃЈ3ЃЉИљОнМЦЫуЪ§ОнСаГіСаСЊБэЃЌМЦЫуГі![]() ЃЌВщБэПЩЕУЁЃ
ЃЌВщБэПЩЕУЁЃ
ЯъНтЃКЃЈЂёЃЉЮваЃЙВга100УћЮФПЦбЇЩњВЮМгПМЪдЃЌЦфжагяЮФПМЪдГЩМЈЕЭгк130ЕФга95%ШЫЃЌгяЮФГЩМЈЬиБ№гХауЕФИХТЪЮЊ![]() ЃЌгяЮФЬиБ№гХауЕФЭЌбЇга
ЃЌгяЮФЬиБ№гХауЕФЭЌбЇга![]() ШЫЃЌЪ§бЇГЩМЈЬиБ№гХауЕФИХТЪЮЊ
ШЫЃЌЪ§бЇГЩМЈЬиБ№гХауЕФИХТЪЮЊ![]() ЃЌЪ§бЇЬиБ№гХауЕФЭЌбЇга
ЃЌЪ§бЇЬиБ№гХауЕФЭЌбЇга![]() ШЫЃЛ
ШЫЃЛ
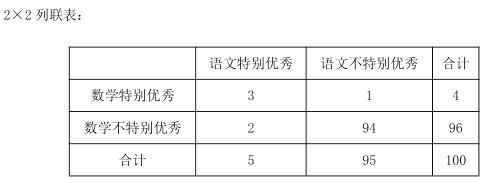
ЃЈЂђЃЉ(i)гяЮФЪ§бЇСНПЦЖМгХауЕФга3ШЫЃЌЕЅПЦгХауЕФга3ШЫЃЌ
МЧСНПЦЖМгХауЕФ3ШЫЗжБ№ЮЊ![]() ЃЌЕЅПЦгХауЕФ3ШЫЗжБ№ЮЊ
ЃЌЕЅПЦгХауЕФ3ШЫЗжБ№ЮЊ![]() ЃЌДгжаЫцЛњГщШЁ2ШЫЃЌЙВгаЃК
ЃЌДгжаЫцЛњГщШЁ2ШЫЃЌЙВгаЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()
![]()
![]() ЙВ15жжЃЌЦфжаетСНШЫГЩМЈЖМгХауЕФга
ЙВ15жжЃЌЦфжаетСНШЫГЩМЈЖМгХауЕФга![]() 3жжЃЌдђетСНШЫСНПЦГЩМЈЖМгХауЕФИХТЪЮЊЃК
3жжЃЌдђетСНШЫСНПЦГЩМЈЖМгХауЕФИХТЪЮЊЃК![]() ЃЛ
ЃЛ
ЃЈiiЃЉ
![]()
![]() га95%ЕФАбЮеШЯЮЊгяЮФЬиБ№гХауЕФЭЌбЇЃЌЪ§бЇвВЬиБ№гХауЃЎ
га95%ЕФАбЮеШЯЮЊгяЮФЬиБ№гХауЕФЭЌбЇЃЌЪ§бЇвВЬиБ№гХауЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]() ЕФРыаФТЪЮЊ
ЕФРыаФТЪЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЮЊЭждВЩЯвЛЕу.
ЮЊЭждВЩЯвЛЕу.
ЃЈ1ЃЉЧѓЭждВCЕФЗНГЬЃЛ
ЃЈ2ЃЉвбжЊСНЬѕЛЅЯрДЙжБЕФжБЯп![]() ЃЌ
ЃЌ![]() ОЙ§ЭждВ
ОЙ§ЭждВ![]() ЕФгвНЙЕу
ЕФгвНЙЕу![]() ЃЌгыЭждВ
ЃЌгыЭждВ![]() НЛгк
НЛгк![]() ЫФЕуЃЌЧѓЫФБпаЮ
ЫФЕуЃЌЧѓЫФБпаЮ![]() УцЛ§ЕФЕФШЁжЕЗЖЮЇ.
УцЛ§ЕФЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЁАХЉМвРжЁБНгД§жааФгаПЭЗП200МфЃЌУПМфШезтН№ЮЊ40дЊЃЌУПЬьЖМПЭТњ.ИљОнЪЕМЪашвЊЃЌИУжааФашЬсИпзтН№ЃЌШчЙћУПМфПЭЗПШезтН№УПдіМг4дЊЃЌПЭЗПГізтОЭЛсМѕЩй10Мф.ЃЈВЛПМТЧЦфЫћвђЫиЃЉ
ЃЈ1ЃЉЩшУПМфПЭЗПШезтН№ЬсИп![]() дЊЃЈ
дЊЃЈ![]() ЃЉЃЌМЧИУжааФПЭЗПЕФШезтН№змЪеШыЮЊ
ЃЉЃЌМЧИУжааФПЭЗПЕФШезтН№змЪеШыЮЊ![]() ЃЌЪдгУ
ЃЌЪдгУ![]() БэЪО
БэЪО![]()
ЃЈ2ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЃЌУПМфПЭЗПШезтН№ЮЊЖрЩйЪБЃЌИУжааФПЭЗПЕФШезтН№змЪеШызюИпЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЕиУцЩЯЭЌвЛЕиЕуЙлВтдЖЗНдШЫйДЙжБЩЯЩ§ЕФШШЦјЧђЃЌдкЩЯЮч10ЕуећШШЦјЧђЕФбіНЧЪЧ![]() ЃЌЕНЩЯЮч10Еу20ЗжЕФбіНЧБфГЩ
ЃЌЕНЩЯЮч10Еу20ЗжЕФбіНЧБфГЩ![]() .ЧыРћгУЯТБэХаЖЯЕНЩЯЮч11ЕуећЪБЃЌШШЦјЧђЕФбіНЧзюНгНќФФИіЖШЪ§( )
.ЧыРћгУЯТБэХаЖЯЕНЩЯЮч11ЕуећЪБЃЌШШЦјЧђЕФбіНЧзюНгНќФФИіЖШЪ§( )
|
|
|
|
|
|
|
|
|
|
| 0.5 | 0.559 | 0.629 | 0.643 | 0.656 | 0.669 | 0.682 | 0.695 | 0.707 |
| 0.866 | 0.829 | 0.777 | 0.766 | 0.755 | 0.743 | 0.731 | 0.719 | 0.707 |
| 0.577 | 0.675 | 0.810 | 0.839 | 0.869 | 0.900 | 0.933 | 0.966 | 1.0 |
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊгНгЯФМОТУгЮЭњМОЕФЕНРДЃЌЩйСжЫТЕЅЖРЩшжУСЫвЛИізЈУХАВХХгЮПЭзЁЫоЕФПЭеЛЃЌЫТУэЕФЙЄзїШЫдБЗЂЯжЮЊгЮПЭзМБИЕФвЛаЉЪГЮягааЉдТЗнЪЃгрВЛЩйЃЌРЫЗбКмбЯжиЃЌЮЊСЫПижЦОгЊГЩБОЃЌМѕЩйРЫЗбЃЌОЭЯыЪЪЪБЕїећЭЖШыЃЎЮЊДЫЫћУЧЭГМЦУПИідТШызЁЕФгЮПЭШЫЪ§ЃЌЗЂЯжУПФъИїИідТЗнРДПЭеЛШызЁЕФгЮПЭШЫЪ§ЛсЗЂЩњжмЦкадЕФБфЛЏЃЌВЂЧвгавдЯТЙцТЩЃК
ЂйУПФъЯрЭЌЕФдТЗнЃЌШызЁПЭеЛЕФгЮПЭШЫЪ§ЛљБОЯрЭЌЃЛ
ЂкШызЁПЭеЛЕФгЮПЭШЫЪ§дк2дТЗнзюЩйЃЌдк8дТЗнзюЖрЃЌЯрВюдМ400ШЫЃЛ
Ђл2дТЗнШызЁПЭеЛЕФгЮПЭдМЮЊ100ШЫЃЌЫцКѓж№дТЕндіжБЕН8дТЗнДяЕНзюЖрЃЎ
ЃЈ1ЃЉЪдгУвЛИіе§ЯваЭШ§НЧКЏЪ§![]() УшЪівЛФъжаШызЁПЭеЛЕФгЮПЭШЫЪ§yгыдТxЗнжЎМфЕФЙиЯЕЃЛ
УшЪівЛФъжаШызЁПЭеЛЕФгЮПЭШЫЪ§yгыдТxЗнжЎМфЕФЙиЯЕЃЛ
ЃЈ2ЃЉЧыЮЪФФМИИідТЗнвЊзМБИ400ЗнвдЩЯЕФЪГЮяЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
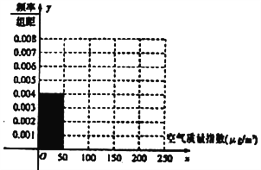
ЁОЬтФПЁПШЋЪРНчдНРДдНЙизЂЛЗОГБЃЛЄЮЪЬтЃЌФГМрВтеОЕугк2018Фъ1дТФГШеЦ№СЌај![]() ЬьМрВтПеЦјжЪСПжИЪ§(
ЬьМрВтПеЦјжЪСПжИЪ§(![]() )ЃЌЪ§ОнЭГМЦШчЯТЃК
)ЃЌЪ§ОнЭГМЦШчЯТЃК
ПеЦјжЪСПжИЪ§( |
|
|
|
|
|
ПеЦјжЪСПЕШМЖ | ПеЦјгХ | ПеЦјСМ | ЧсЖШЮлШО | жаЖШЮлШО | жиЖШЮлШО |
ЬьЪ§ | 20 | 40 |
| 10 | 5 |
ЃЈ1ЃЉИљОнЫљИјЭГМЦБэКЭЦЕТЪЗжВМжБЗНЭМжаЕФаХЯЂЧѓГі![]() ЃЌ
ЃЌ![]() ЕФжЕЃЌВЂЭъГЩЦЕТЪЗжВМжБЗНЭМЃЛ
ЕФжЕЃЌВЂЭъГЩЦЕТЪЗжВМжБЗНЭМЃЛ
ЃЈ2ЃЉгЩЦЕТЪЗжВМжБЗНЭМЃЌЧѓИУзщЪ§ОнЕФжкЪ§КЭжаЮЛЪ§ЃЛ
ЃЈ3ЃЉдкПеЦјжЪСПжИЪ§ЗжБ№Ъєгк![]() КЭ
КЭ![]() ЕФМрВтЪ§ОнжаЃЌгУЗжВуГщбљЕФЗНЗЈГщШЁ
ЕФМрВтЪ§ОнжаЃЌгУЗжВуГщбљЕФЗНЗЈГщШЁ![]() ЬьЃЌдйДгжаШЮвтбЁШЁ
ЬьЃЌдйДгжаШЮвтбЁШЁ![]() ЬьЃЌЧѓЪТМў
ЬьЃЌЧѓЪТМў![]() ЁАСНЬьПеЦјЖМЮЊСМЁБЗЂЩњЕФИХТЪ.
ЁАСНЬьПеЦјЖМЮЊСМЁБЗЂЩњЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхдкЃЈ0ЃЌ+ЁоЃЉЩЯЕФКЏЪ§fЃЈxЃЉЕФЕМЪ§![]() Тњзуx2
Тњзуx2![]() ЃМ1ЃЌдђЯТСаВЛЕШЪНжавЛЖЈГЩСЂЕФЪЧЃЈЁЁЁЁЃЉ
ЃМ1ЃЌдђЯТСаВЛЕШЪНжавЛЖЈГЩСЂЕФЪЧЃЈЁЁЁЁЃЉ
A.fЃЈ![]() ЃЉ+1ЃМfЃЈ
ЃЉ+1ЃМfЃЈ![]() ЃЉЃМfЃЈ
ЃЉЃМfЃЈ![]() ЃЉЉ1B.fЃЈ
ЃЉЉ1B.fЃЈ![]() ЃЉ+1ЃМfЃЈ
ЃЉ+1ЃМfЃЈ![]() ЃЉЃМfЃЈ
ЃЉЃМfЃЈ![]() ЃЉЉ1
ЃЉЉ1
C.fЃЈ![]() ЃЉЉ1ЃМfЃЈ
ЃЉЉ1ЃМfЃЈ![]() ЃЉЃМfЃЈ
ЃЉЃМfЃЈ![]() ЃЉ+1D.fЃЈ
ЃЉ+1D.fЃЈ![]() ЃЉЉ1ЃМfЃЈ
ЃЉЉ1ЃМfЃЈ![]() ЃЉЃМfЃЈ
ЃЉЃМfЃЈ![]() ЃЉ+1
ЃЉ+1
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉЃНalnxЉexЃЈaЁЪRЃЉЃЎЦфжаeЪЧздШЛЖдЪ§ЕФЕзЪ§ЃЎ
ЃЈ1ЃЉЬжТлКЏЪ§fЃЈxЃЉЕФЕЅЕїадВЂЧѓМЋжЕЃЛ
ЃЈ2ЃЉСюКЏЪ§gЃЈxЃЉЃНfЃЈxЃЉ+exЃЌШєxЁЪ[1ЃЌ+ЁоЃЉЪБЃЌgЃЈxЃЉЁн0ЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕу![]() ЗжБ№ЪЧдВаФдкдЕуЃЌАыОЖЮЊ
ЗжБ№ЪЧдВаФдкдЕуЃЌАыОЖЮЊ![]() КЭ
КЭ![]() ЕФдВЩЯЕФЖЏЕу.ЖЏЕу
ЕФдВЩЯЕФЖЏЕу.ЖЏЕу![]() ДгГѕЪМЮЛжУ
ДгГѕЪМЮЛжУ![]() ПЊЪМЃЌАДФцЪБеыЗНЯђвдНЧЫйЖШ
ПЊЪМЃЌАДФцЪБеыЗНЯђвдНЧЫйЖШ![]() зїдВжмдЫЖЏЃЌЭЌЪБЕу
зїдВжмдЫЖЏЃЌЭЌЪБЕу![]() ДгГѕЪМЮЛжУ
ДгГѕЪМЮЛжУ![]() ПЊЪМЃЌАДЫГЪБеыЗНЯђвдНЧЫйЖШ
ПЊЪМЃЌАДЫГЪБеыЗНЯђвдНЧЫйЖШ![]() зїдВжмдЫЖЏ.МЧ
зїдВжмдЫЖЏ.МЧ![]() ЪБПЬЃЌЕу
ЪБПЬЃЌЕу![]() ЕФзнзјБъЗжБ№ЮЊ
ЕФзнзјБъЗжБ№ЮЊ![]() .
.
ЃЈЂёЃЉЧѓ![]() ЪБПЬЃЌ
ЪБПЬЃЌ![]() СНЕуМфЕФОрРыЃЛ
СНЕуМфЕФОрРыЃЛ
ЃЈЂђЃЉЧѓ![]() ЙигкЪБМф
ЙигкЪБМф![]() ЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓЕБ
ЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓЕБ![]() ЪБЃЌетИіКЏЪ§ЕФжЕгђ.
ЪБЃЌетИіКЏЪ§ЕФжЕгђ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com