
【题目】以直角坐标系原点O为极点,x轴的正半轴为极轴.已知点P的直角坐标为![]() ,点M的极坐标为
,点M的极坐标为![]() ,若直线l过点P,且倾斜角为
,若直线l过点P,且倾斜角为![]() ,圆C以M点为圆心,4为半径.
,圆C以M点为圆心,4为半径.
![]() 求直线l和圆C的极坐标方程;
求直线l和圆C的极坐标方程;
![]() 直线l与x轴y轴分别交于A,B两点,Q为圆C上一动点,求
直线l与x轴y轴分别交于A,B两点,Q为圆C上一动点,求![]() 面积的最小值.
面积的最小值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】用一个长为![]() ,宽为
,宽为![]() 的矩形铁皮(如图1)制作成一个直角圆形弯管(如图3):先在矩形的中间画一条曲线,并沿曲线剪开,将所得的两部分分别卷成体积相等的斜截圆柱状(如图2),然后将其中一个适当翻转拼接成直角圆形弯管(如图3)(不计拼接损耗部分),并使得直角圆形弯管的体积最大;
的矩形铁皮(如图1)制作成一个直角圆形弯管(如图3):先在矩形的中间画一条曲线,并沿曲线剪开,将所得的两部分分别卷成体积相等的斜截圆柱状(如图2),然后将其中一个适当翻转拼接成直角圆形弯管(如图3)(不计拼接损耗部分),并使得直角圆形弯管的体积最大;
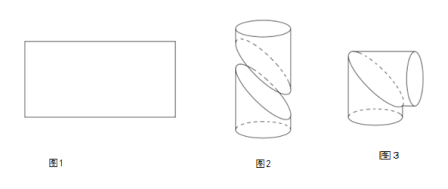
(1)求直角圆形弯管(图3)的体积;
(2)求斜截面椭圆的焦距;
(3)在相应的图1中建立适当的坐标系,使所画的曲线的方程为![]() ,求出方程并画出大致图像;
,求出方程并画出大致图像;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形![]() 是一个历史文物展览厅的俯视图,点
是一个历史文物展览厅的俯视图,点![]() 在
在![]() 上,在梯形
上,在梯形![]() 区域内部展示文物,
区域内部展示文物,![]() 是玻璃幕墙,游客只能在
是玻璃幕墙,游客只能在![]() 区域内参观.在
区域内参观.在![]() 上点
上点![]() 处安装一可旋转的监控摄像头.
处安装一可旋转的监控摄像头.![]() 为监控角,其中
为监控角,其中![]() 、
、![]() 在线段
在线段![]() (含端点)上,且点
(含端点)上,且点![]() 在点
在点![]() 的右下方.经测量得知:
的右下方.经测量得知:![]() 米,
米,![]() 米,
米,![]() 米,
米,![]() .记
.记![]() (弧度),监控摄像头的可视区域
(弧度),监控摄像头的可视区域![]() 的面积为
的面积为![]() 平方米.
平方米.

(1)求![]() 关于
关于![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;(参考数据:
的取值范围;(参考数据:![]() )
)
(2)求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某游戏棋盘上标有第![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 站,棋子开始位于第
站,棋子开始位于第![]() 站,选手抛掷均匀硬币进行游戏,若掷出正面,棋子向前跳出一站;若掷出反面,棋子向前跳出两站,直到跳到第
站,选手抛掷均匀硬币进行游戏,若掷出正面,棋子向前跳出一站;若掷出反面,棋子向前跳出两站,直到跳到第![]() 站或第
站或第![]() 站时,游戏结束.设游戏过程中棋子出现在第
站时,游戏结束.设游戏过程中棋子出现在第![]() 站的概率为
站的概率为![]() .
.
(1)当游戏开始时,若抛掷均匀硬币![]() 次后,求棋子所走站数之和
次后,求棋子所走站数之和![]() 的分布列与数学期望;
的分布列与数学期望;
(2)证明:![]() ;
;
(3)若最终棋子落在第![]() 站,则记选手落败,若最终棋子落在第
站,则记选手落败,若最终棋子落在第![]() 站,则记选手获胜.请分析这个游戏是否公平.
站,则记选手获胜.请分析这个游戏是否公平.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)若对任意的![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 的最小值为
的最小值为![]() ,求实数
,求实数![]() 的值;
的值;
(3)若对任意实数![]() 、
、![]() 、
、![]() ,均存在以
,均存在以![]() 、
、![]() 、
、![]() 为三边边长的三角形,求实数
为三边边长的三角形,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数的对称性有如下结论:对于给定的函数![]() ,如果对于任意的
,如果对于任意的![]() 都有
都有![]() 成立
成立![]() 为常数),则函数
为常数),则函数![]() 关于点
关于点![]() 对称.
对称.
(1)用题设中的结论证明:函数![]() 关于点
关于点![]() ;
;
(2)若函数![]() 既关于点
既关于点![]() 对称,又关于点
对称,又关于点![]() 对称,且当
对称,且当![]() 时,
时,![]() ,求:①
,求:①![]() 的值;
的值;
②当![]() 时,
时,![]() 的表达式.
的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:极坐标与参数方程
已知在平面直角坐标系xOy中,O为坐标原点,曲线C: 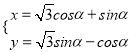 (α为参数),在以平面直角坐标系的原点为极点,x轴的正半轴为极轴,取相同单位长度的极坐标系,直线l:ρ
(α为参数),在以平面直角坐标系的原点为极点,x轴的正半轴为极轴,取相同单位长度的极坐标系,直线l:ρ![]() .
.
(Ⅰ)求曲线C的普通方程和直线l的直角坐标方程;
(Ⅱ)曲线C上恰好存在三个不同的点到直线l的距离相等,分别求出这三个点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
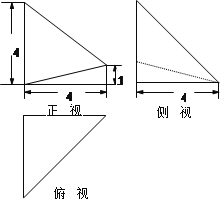
已知几何体A—BCED的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
(1)求此几何体的体积V的大小;
(2)求异面直线DE与AB所成角的余弦值;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com