
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的面积.
的面积.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某市公交公司为了鼓励广大市民绿色出行,计划在某个地段增设一个起点站,为了研究车辆发车的间隔时间![]() 与乘客等候人数
与乘客等候人数![]() 之间的关系,经过抽样调查五个不同时段的情形,统计得到如下数据:
之间的关系,经过抽样调查五个不同时段的情形,统计得到如下数据:
间隔时间( | 8 | 10 | 12 | 14 | 16 |
等候人数( | 16 | 19 | 23 | 26 | 29 |
调查小组先从这5组数据中选取其中的4组数据求得线性回归方程,再用剩下的1组数据进行检验,检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数![]() ,再求
,再求![]() 与实际等候人数
与实际等候人数![]() 的差,若差值的绝对值不超过1,则称所求的回归方程是“理想回归方程”.
的差,若差值的绝对值不超过1,则称所求的回归方程是“理想回归方程”.
(1)若选取的是前4组数据,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并判断所求方程是否是“理想回归方程”;
,并判断所求方程是否是“理想回归方程”;
(2)为了使等候的乘客不超过38人,试用所求方程估计间隔时间最多可以设为多少分钟?
参考公式:用最小二乘法求线性回归方程![]() 的系数公式:
的系数公式:
 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学团委组织了“纪念抗日战争胜利73周年”的知识竞赛,从参加竞赛的学生中抽出60名学生,将其成绩(均为整数)分成六段![]() ,
,![]() ,…,
,…,![]() 后,画出如图所示的部分频率分布直方图.观察图形给出的信息,回答下列问题:
后,画出如图所示的部分频率分布直方图.观察图形给出的信息,回答下列问题:
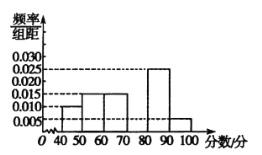
(1)求第四组的频率,并补全这个频率分布直方图;
(2)估计这次竞赛的及格率(60分及以上为及格)和平均分(同一组中的数据用该组区间的中点值代表)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了确定下一年度投入某种产品的宣传费用,需了解年宣传费![]() (单位:万元)对年销量
(单位:万元)对年销量![]() (单位:吨)和年利润(单位:万元)的影响.对近6年宣传费
(单位:吨)和年利润(单位:万元)的影响.对近6年宣传费![]() 和年销量
和年销量![]() 的数据做了初步统计,得到如下数据:
的数据做了初步统计,得到如下数据:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年宣传费x(万元) | 38 | 48 | 58 | 68 | 78 | 88 |
年销售量y(吨) | 16.8 | 18.8 | 20.7 | 22.4 | 24.0 | 25.5 |
经电脑模拟,发现年宣传费![]() (万元)与年销售量
(万元)与年销售量![]() (吨)之间近似满足关系式
(吨)之间近似满足关系式![]() 即
即![]() ,对上述数据作了初步处理,得到相关的值如下表:
,对上述数据作了初步处理,得到相关的值如下表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(Ⅰ)从表中所给出的6年年销售量数据中任选2年做年销售量的调研,求所选数据中至多有一年年销售量低于20吨的概率.
(Ⅱ)根据所给数据,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(Ⅲ)若生产该产品的固定成本为200(万元),且每生产1(吨)产品的生产成本为20(万元)(总成本=固定成本+生产成本+年宣传费),销售收入为![]() (万元),假定该产品产销平衡(即生产的产品都能卖掉),2019年该公司计划投入
(万元),假定该产品产销平衡(即生产的产品都能卖掉),2019年该公司计划投入![]() 万元宣传费,你认为该决策合理吗?请说明理由.(其中
万元宣传费,你认为该决策合理吗?请说明理由.(其中![]() 为自然对数的底数,
为自然对数的底数,![]() )
)
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为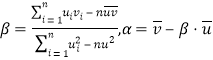 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中华民族是一个传统文化丰富多彩的民族,各民族有许多优良的传统习俗,如过大年吃饺子,元宵节吃汤圆,端午节吃粽子,中秋节吃月饼等等,让人们感受到浓浓的节目味道. 某小区有1200户家庭,全部居民在小区的8栋楼内,各家庭在过年时各自包有肉馅饺子、蛋馅饺子和素馅饺子三种味道的饺子(假设每个家庭包有且只包有这三种味道中的一种味道的饺子).
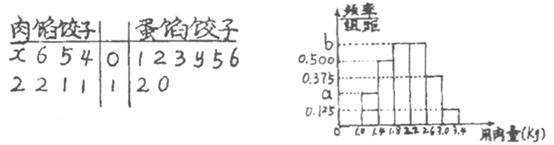
(1)现根据饺子的不同味道用分层抽样的方法从该小区随机抽样抽取![]() 户家庭,其中有10户家庭包的是素馅饺子,在抽取家庭中包肉馅饺子和蛋馅饺子的家庭分布在8栋楼内的住户数记录为如图所示的茎叶图,已知肉馅饺子数的中位数为10,蛋馅饺子数的平均数为5,求该小区包肉馅饺子的户数;
户家庭,其中有10户家庭包的是素馅饺子,在抽取家庭中包肉馅饺子和蛋馅饺子的家庭分布在8栋楼内的住户数记录为如图所示的茎叶图,已知肉馅饺子数的中位数为10,蛋馅饺子数的平均数为5,求该小区包肉馅饺子的户数;
(2)现从包肉馅饺子的家庭中随机抽取100个家庭调查包饺子的用肉量(单位: ![]() )得到了如图所示的频率分布直方图,若用肉量在第1小组
)得到了如图所示的频率分布直方图,若用肉量在第1小组![]() 内的户数为
内的户数为![]() (
(![]() 为茎叶图中的
为茎叶图中的![]() ),试估计该小区过年时各户用于包饺子的平均用肉量(各小组数据以组中值为代表).
),试估计该小区过年时各户用于包饺子的平均用肉量(各小组数据以组中值为代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在
是定义在![]() 上的偶函数,且当
上的偶函数,且当![]() 时,
时, ![]() .现已画出函数
.现已画出函数![]() 在
在![]() 轴左侧的图象,如图所示,并根据图象:
轴左侧的图象,如图所示,并根据图象:

(1)直接写出函数![]() ,
, ![]() 的增区间;
的增区间;
(2)写出函数![]() ,
, ![]() 的解析式;
的解析式;
(3)若函数![]() ,
, ![]() ,求函数
,求函数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
函数![]() 是定义在
是定义在![]() 上的奇函数,且
上的奇函数,且![]() 。
。
(1)求实数a,b,并确定函数![]() 的解析式;
的解析式;
(2)判断![]() 在(-1,1)上的单调性,并用定义证明你的结论;
在(-1,1)上的单调性,并用定义证明你的结论;
(3)写出![]() 的单调减区间,并判断
的单调减区间,并判断![]() 有无最大值或最小值?如有,写出最大值或最小值。(本小问不需要说明理由)
有无最大值或最小值?如有,写出最大值或最小值。(本小问不需要说明理由)
查看答案和解析>>
科目:高中数学 来源: 题型:
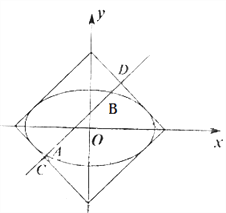
【题目】如图,曲线![]() 与正方形
与正方形![]() :
: ![]() 的边界相切.
的边界相切.
(1)求![]() 的值;
的值;
(2)设直线![]() 交曲线
交曲线![]() 于
于![]() ,交
,交![]() 于
于![]() ,是否存在这样的曲线
,是否存在这样的曲线![]() ,使得
,使得![]() ,
, ![]() ,
, ![]() 成等差数列?若存在,求出实数
成等差数列?若存在,求出实数![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com