
(12分)
已知斜三棱柱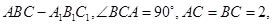
 在底面
在底面 上的射影恰为
上的射影恰为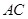 的中点
的中点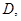 又知
又知 ;
;

(1)求证: 平面
平面 ;
;
(2)求 到平面
到平面 的距离;
的距离;
(3)求二面角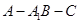 的余弦值;
的余弦值;
(1) 略
(2) 略
(3) 
【解析】(1)∵A1在底面ABC上的射影为AC的中点D
∴平面A1ACC1⊥平面ABC∵BC⊥AC且平面A1ACC1∩平面ABC=AC
∴BC⊥平面A1ACC1 ∴BC⊥AC1
∵AC1⊥BA1且BC∩BA1=B ∴AC1⊥平面A1BC ----------4分
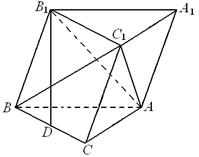
(2)如图所示,以C为坐标原点建立空间直角坐标系

∵AC1⊥平面A1BC ∴AC1⊥A1C
∴四边形A1ACC1是菱形 ∵D是AC中点
∴∠A1AD=60°∴A(2,0,0) A1(1,0,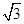 ) B(0,2,0)
) B(0,2,0)
C1(-1,0,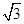 ) ∴
) ∴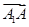 =(1,0,
=(1,0,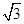 )
) 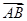 =(-2,2,0)
=(-2,2,0)
设平面A1AB的法向量 =(x,y,z) ∴
=(x,y,z) ∴ 令z=1 ∴
令z=1 ∴ =(
=(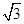 ,
,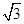 ,1)
,1)
∵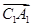 =(2,0,0) ∴
=(2,0,0) ∴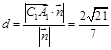 ∴C1到平面A1AB的距离是
∴C1到平面A1AB的距离是 --8分
--8分
(3)平面A1AB的法向量 =(
=(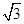 ,
,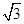 ,1) 平面A1BC的法向量
,1) 平面A1BC的法向量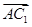 =(-3,0,
=(-3,0,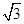 )
)
∴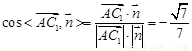 设二面角A-A1B-C的平面角为
设二面角A-A1B-C的平面角为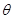 ,
,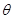 为锐角,
为锐角,
∴ ∴二面角A-A1B-C的余弦值为
∴二面角A-A1B-C的余弦值为 ---------------12分
---------------12分


科目:高中数学 来源:2014届河北省高三上学期第一次月考理科数学试卷(解析版) 题型:解答题
已知斜三棱柱 的底面是直角三角形,
的底面是直角三角形, 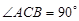 ,侧棱与底面所成角为
,侧棱与底面所成角为 ,点
,点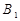 在底面上的射影
在底面上的射影 落在
落在 上.
上.

(1)求证: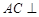 平面
平面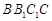 ;
;
(2)若 ,且当
,且当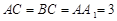 时,求二面角
时,求二面角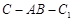 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年甘肃省高三第二次诊断性考试理科数学试卷 题型:解答题
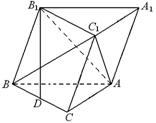
(本题满分12分)已知斜三棱柱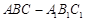 的底面是直角三角形,
的底面是直角三角形,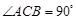 ,侧棱与底面所成角为
,侧棱与底面所成角为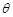 ,点
,点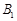 在底面上射影D落在BC上.
在底面上射影D落在BC上.
(Ⅰ)求证: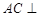 平面
平面 ;
;
(Ⅱ)若点D恰为BC中点,且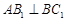 ,求
,求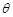 的大小;
的大小;
(III)若 ,且当
,且当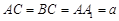 时,求二面角
时,求二面角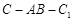 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省高三下学期开学考试理科数学 题型:解答题
(本题满分12分)已知斜三棱柱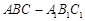 的底面是直角三角形,
的底面是直角三角形,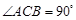 ,侧棱与底面所成角为
,侧棱与底面所成角为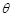 ,点
,点 在底面上射影D落在BC上.
在底面上射影D落在BC上.
(Ⅰ)求证: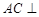 平面
平面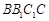 ;
;
(Ⅱ)若点D恰为BC中点,且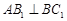 ,求
,求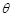 的大小;
的大小;
(III)若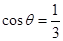 ,且当
,且当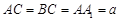 时,求二面角
时,求二面角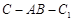 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源:2013届江西省高二周六强化训练(一)数学 题型:解答题
(本题满分12分)已知斜三棱柱 的底面是直角三角形,
的底面是直角三角形, ,侧棱与底面所成角为
,侧棱与底面所成角为 ,点
,点 在底面上射影D落在BC上.
在底面上射影D落在BC上.

(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)若点D恰为BC中点,且 ,求
,求 的大小;
的大小;
(III)若 ,且当
,且当 时,求二面角
时,求二面角 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com