解:不妨设函数g(x)=e
x,
(Ⅰ)∵f′(x)=λg′[λx+(1-λ)a]-λg′(x),
由f′(x)>0得,g′[λx+(1-λ)a]>g′(x),
∴λx+(1-λ)a>x,即(1-λ)(x-a)<0,解得x<a,
故当x<a时,f′(x)>0;当x>a时,f′(x)<0;
∴当x=a时,f(x)取极大值f(a)=(1-λ)e
a,但f(x)没有极小值.
(Ⅱ)∵
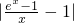
=
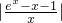
,
又当x>0时,令h(x)=e
x-x-1,则h′(x)=e
x-1>0,故h(x)>h(0)=0,
因此原不等式化为
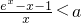
,即e
x-(1+a)x-1<0,
令g(x)=e
x-(1+a)x-1,则g′(x)=e
x-(1+a),
由g′(x)=0得:e
x=1+a,解得x=ln(1+a),
当0<x<ln(1+a)时,g′(x)<0;当x>ln(1+a)时,g′(x)>0,
故当x=ln(1+a)时,g(x)取最小值g[ln(1+a)]=a-(1+a)ln(1+a),
令s(a)=
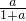
-ln(1+a),a>0,则s′(a)=
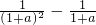
=-
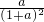
<0,
故s(a)<s(0)=0,即g[ln(1+a)]=a-(1+a)ln(1+a)<0,
因此,存在正数x=ln(1+a),使原不等式成立;
(Ⅲ)对任意正数a
1,a
2,存在实数x
1,x
2使
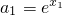
,
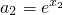
,
则
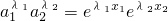
=
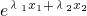
,λ
1a
1+λ
2a
2=
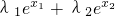
,
原不等式
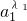
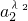
≤λ
1a
1+λ
2a
2?
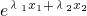
≤
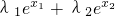
?g(λ
1x
1+λ
2x
2)≤λ
1g(x
1)+λ
2g(x
2),
由(1)f(x)≤(1-λ)g(a)恒成立,故g[λx+(1-λ)a]≤λg(x)+(1-λ)g(a),
取x=x
1,a=x
2,λ=λ
1,1-λ=λ
2,即得g(λ
1x
1+λ
2x
2)≤λ
1g(x
1)+λ
2g(x
2),即
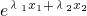
≤
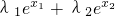
,
故所证不等式成立.
分析:(I)令g(x)=e
x,求导数f′(x),根据g′(x)的单调性,解不等式f′(x)>0,f′(x)<0可得函数f(x)的单调区间,由极值定义可得极值;
(II)当x>0时,令h(x)=e
x-x-1,利用导数可判断h(x)的符号,从而可去掉绝对值号,则不等式变为e
x-(1+a)x-1<0,令g(x)=e
x-(1+a)x-1,存在正数x使不等式成立,等价于g(x)
min<0,利用导数可求得g(x)
min=a-(1+a)ln(1+a),令s(a)=
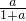
-ln(1+a),对任意给定的正实数a不等式成立,等价于s(a)
max<0,用导数易证明;
(III)对任意正数a
1,a
2,存在实数x
1,x
2使
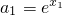
,
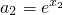
,原不等式
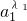
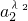
≤λ
1a
1+λ
2a
2?g(λ
1x
1+λ
2x
2)≤λ
1g(x
1)+λ
2g(x
2),由(1)f(x)≤(1-λ)g(a)恒成立,得g[λx+(1-λ)a]≤λg(x)+(1-λ)g(a),在该不等式中适当赋值即可证明;
点评:本题考查利用导数研究函数的最值、极值,考查学生综合运用知识分析解决问题的能力,本题综合性强,难度大,对能力要求较高.

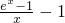 |<a成立?若存在,求出x,若不存在,说明理由;
|<a成立?若存在,求出x,若不存在,说明理由;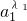
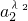 ≤λ1a1+λ2a2.
≤λ1a1+λ2a2.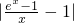 =
=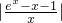 ,
,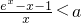 ,即ex-(1+a)x-1<0,
,即ex-(1+a)x-1<0,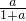 -ln(1+a),a>0,则s′(a)=
-ln(1+a),a>0,则s′(a)=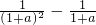 =-
=-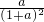 <0,
<0,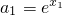 ,
,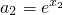 ,
,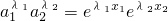 =
=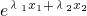 ,λ1a1+λ2a2=
,λ1a1+λ2a2=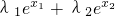 ,
,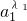
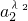 ≤λ1a1+λ2a2?
≤λ1a1+λ2a2?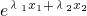 ≤
≤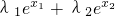 ?g(λ1x1+λ2x2)≤λ1g(x1)+λ2g(x2),
?g(λ1x1+λ2x2)≤λ1g(x1)+λ2g(x2),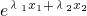 ≤
≤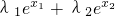 ,
,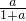 -ln(1+a),对任意给定的正实数a不等式成立,等价于s(a)max<0,用导数易证明;
-ln(1+a),对任意给定的正实数a不等式成立,等价于s(a)max<0,用导数易证明;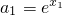 ,
,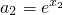 ,原不等式
,原不等式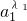
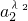 ≤λ1a1+λ2a2?g(λ1x1+λ2x2)≤λ1g(x1)+λ2g(x2),由(1)f(x)≤(1-λ)g(a)恒成立,得g[λx+(1-λ)a]≤λg(x)+(1-λ)g(a),在该不等式中适当赋值即可证明;
≤λ1a1+λ2a2?g(λ1x1+λ2x2)≤λ1g(x1)+λ2g(x2),由(1)f(x)≤(1-λ)g(a)恒成立,得g[λx+(1-λ)a]≤λg(x)+(1-λ)g(a),在该不等式中适当赋值即可证明;

 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案