
����Ŀ����ij�����������ȡ10����ͥ����õ�i����ͥ��������xi(��λ��ǧԪ)���´���yi(��λ��ǧԪ)���������ϣ����![]() ��80��
��80�� ![]() ��20��
��20�� ![]() ��184��
��184�� ![]() ��720.
��720.
(1)���ͥ���´���y��������x�����Իع鷽��y��bx��a��
(2)�жϱ���x��y֮��������ػ��Ǹ���أ�
(3)���þ�����ij��ͥ������Ϊ7ǧԪ��Ԥ��ü�ͥ���´��
�������Իع鷽��y��bx��a�У�  ��a��
��a��![]() ��b
��b![]() ������
������![]() ��
�� ![]() Ϊ����ƽ��ֵ��
Ϊ����ƽ��ֵ��
���𰸡�(1) y��0.3x��0.4(2)�����(3) 1.7(ǧԪ)��
�����������������(1)�ȸ���������������������ĵ�����꣬�ٸ����������������ʽ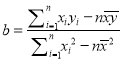 ����Ҫ���й������Ӷ��ɵõ�
����Ҫ���й������Ӷ��ɵõ�![]() ��ֵ�����������ĵ���������ع鷽�̼��ɵõ�
��ֵ�����������ĵ���������ع鷽�̼��ɵõ�![]() ��ֵ����������ûع鷽�̣���2��������ع鷽�̵�б�ʵ����������ж���������������ػ��Ǹ���أ���3��
��ֵ����������ûع鷽�̣���2��������ع鷽�̵�б�ʵ����������ж���������������ػ��Ǹ���أ���3��![]() ��������ع鷽�̿�Ԥ��ü�ͥ���´��
��������ع鷽�̿�Ԥ��ü�ͥ���´��
(1)������֪n��10�� ![]() ��
��![]() ��
��![]() ��8��
��8�� ![]() ��
��![]() ��
��![]() ��2.
��2.
��lxx��![]() ��n
��n![]() 2��720��10��82��80��
2��720��10��82��80��
lxy��![]() yi��n
yi��n![]()
![]() ��184��10��8��2��24.
��184��10��8��2��24.
�ɴ˵�b��![]() ��0.3��a��
��0.3��a��![]() ��b
��b![]() ��2��0.3��8����0.4��
��2��0.3��8����0.4��
������ع鷽��Ϊy��0.3x��0.4.
(2)���ڱ���y��ֵ��x��ֵ���Ӷ�����(b��0.3>0)����x��y֮��������أ�
(3)��x��7����ع鷽�̿���Ԥ��ü�ͥ���´���Ϊ
y��0.3��7��0.4��1.7(ǧԪ)��
���������硿������Ҫ�������Իع鷽�̼���Ӧ�ã���������.��ع�ֱ�߷��̵IJ��裺�������������ݻ���ɢ��ͼ��ȷ��������������������ع�ϵ���ڼ���![]() ��ֵ���ۼ���ع�ϵ��
��ֵ���ۼ���ع�ϵ��![]() ����д���ع�ֱ�߷���Ϊ
����д���ع�ֱ�߷���Ϊ![]() �� �ع�ֱ�߹�����������
�� �ع�ֱ�߹�����������![]() ��һ����Ҫ���ʣ��������Իع鷽�̿��Թ������壬�������Ƿ������������ı仯����.
��һ����Ҫ���ʣ��������Իع鷽�̿��Թ������壬�������Ƿ������������ı仯����.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �ϵĵ㵽��
�ϵĵ㵽��![]() �ľ��������ֱ��
�ľ��������ֱ��![]() �ľ���С2.
�ľ���С2.
��1��������![]() �ķ��̣�
�ķ��̣�
��2������![]() ��б��Ϊ
��б��Ϊ![]() ��ֱ��
��ֱ��![]() ������
������![]() ��
��![]() ��
�� ![]() ���㣬��
���㣬��![]() ����
����![]() ʱ����
ʱ����![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��![]() ����Բ
����Բ![]() �ij��᳤�Ƕ��᳤��2����
�ij��᳤�Ƕ��᳤��2����![]() ����Բ
����Բ![]() ���ҽ��㣬ֱ��
���ҽ��㣬ֱ��![]() ��б��Ϊ
��б��Ϊ![]() ��
��![]() Ϊ����ԭ��.
Ϊ����ԭ��.
��1������Բ![]() �ķ��̣�
�ķ��̣�
��2�������![]() �Ķ�ֱ��
�Ķ�ֱ��![]() ����Բ
����Բ![]() �ཻ��
�ཻ��![]() ����.��
����.��![]() ��������ʱ����ֱ��
��������ʱ����ֱ��![]() �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������![]() ��
��![]() ����ͬ������ɣ�
����ͬ������ɣ� ![]() Ϊ
Ϊ![]() ��ǰ
��ǰ![]() ��ͣ���������
��ͣ���������![]() ��
��![]() �����ֵΪ__________��
�����ֵΪ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪ԲC��y�������ڵ�T(0,2)����x��������ύ������![]() (��
(��![]() �ڵ�
�ڵ�![]() �����)����
�����)����![]() .
.
(1)��ԲC�ķ��̣�(2)����![]() ����һֱ����ԲO��
����һֱ����ԲO�� ![]() �ཻ��
�ཻ��![]() ���㣬����
���㣬����![]() ����֤��
����֤�� ![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
�� ![]() .
.
��1����![]() �ֱ��ʾ��һö�ʵؾ��ȵ����������ӣ�������ĵ����ֱ�Ϊ1,2,3,4,5,6�����Ⱥ���������ʱ��һ�Ρ��ڶ��γ��ֵĵ�����������
�ֱ��ʾ��һö�ʵؾ��ȵ����������ӣ�������ĵ����ֱ�Ϊ1,2,3,4,5,6�����Ⱥ���������ʱ��һ�Ρ��ڶ��γ��ֵĵ�����������![]() �ĸ��ʣ�
�ĸ��ʣ�
��2����![]() ����������
����������![]() ��ȡֵ��������
��ȡֵ��������![]() �ĸ���.
�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������f��x���Ķ�����Ϊ[��1��1]��ͼ����ͼ1��ʾ������g��x���Ķ�����Ϊ[��2��2]��ͼ����ͼ2��ʾ���躯��f��g��x������m����㣬����g��f��x������n����㣬��m+n���ڣ�������
A. 6 B. 10 C. 8 D. 1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
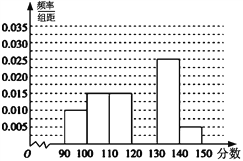
����Ŀ��������ѧ�Ӳμ����μƻ������������Ե�ѧ���������ȡ60��ѧ����������ѧ�ɼ�����Ϊ�������ֳ�����![]() ��
�� ![]() ������
������ ![]() ��õ����²���Ƶ�ʷֲ�ֱ��ͼ���۲�ͼ�ε���Ϣ���ش��������⣺
��õ����²���Ƶ�ʷֲ�ֱ��ͼ���۲�ͼ�ε���Ϣ���ش��������⣺
��1���������![]() �ڵ�Ƶ�ʣ�
�ڵ�Ƶ�ʣ�
��2�����Ʊ��ο��Գɼ�����λ��������������룬������������
��3���÷ֲ�����ķ����ڷ�����Ϊ![]() ��ѧ���г�ȡһ������Ϊ6��������������������һ�����壬������ȡ2�ˣ���������
��ѧ���г�ȡһ������Ϊ6��������������������һ�����壬������ȡ2�ˣ���������![]() ���ڷ�����
���ڷ�����![]() �ڵĸ���.
�ڵĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() Ϊʵ��������
Ϊʵ��������![]() ��
��
��1����![]() ����
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2������![]() �ĵ����ԣ�
�ĵ����ԣ�
��3����![]() ʱ������
ʱ������![]() ������
������![]() �ڵ���������
�ڵ���������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com