
【题目】已知椭圆E:![]() +
+![]() =1(a>b>0),其左右焦点为F1,F2,过F2的直线l交椭圆E于A,B两点,△AB F1的周长为8,且△AF1F2的面积最大时,△AF1F2为正三角形。
=1(a>b>0),其左右焦点为F1,F2,过F2的直线l交椭圆E于A,B两点,△AB F1的周长为8,且△AF1F2的面积最大时,△AF1F2为正三角形。
(1)求椭圆E的方程;
(2)若MN是椭圆E经过 原点的弦,MN||AB,求证: ![]() 为定值
为定值
【答案】(1)![]() (2)4
(2)4
【解析】试题分析:(I)根据题意列出关于![]() 、
、![]() 、
、![]() 的方程组,结合性质
的方程组,结合性质![]() , 求出
, 求出![]() 、
、![]() 、
、![]() ,即可得结果;(Ⅱ)直线与曲线联立,根据韦达定理,弦长公式将
,即可得结果;(Ⅱ)直线与曲线联立,根据韦达定理,弦长公式将![]() 用
用![]() 表示,消去
表示,消去![]() 即可得结果.
即可得结果.
试题解析:(I)由已知A,B在椭圆上,可得|AF1|+|AF2|=|BF1|=|BF2|=2a,
又△ABF1的周长为8,所以|AF1|+|AF2|+|BF1|=|BF2|=4a=8,即a=2,
由椭圆的对称性可得,△AF1F2为正三角形当且仅当A为椭圆短轴顶点,
则a=2c,即c=1,b2=a2﹣c2=3,
则椭圆C的方程为![]()
(Ⅱ)证明:若直线l的斜率不存在,即l:x=1,求得|AB|=3,|MN|=2![]() ,可得
,可得![]() =4;
=4;
若直线l的斜率存在,设直线l:y=k(x﹣1),
设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),
代入椭圆方程![]() +
+![]() ,可得(3+4k2)x2﹣8k2x+4k2﹣12=0,
,可得(3+4k2)x2﹣8k2x+4k2﹣12=0,
有x1+x2 =![]() ,x1x2=
,x1x2=![]() ,
,
|AB|![]() ,
,
由y=kx代入椭圆方程,可得x=±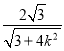 ,
,
|MN|=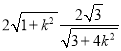
即有![]() =4.
=4.
综上可得![]() 为定值4.
为定值4.


科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的离心率为
的离心率为![]() ,短轴的一个端点到右焦点的距离为
,短轴的一个端点到右焦点的距离为![]() .
.
(1)求椭圆C的方程;
(2)设直线l与椭圆C交于A、B两点,坐标原点O到直线l的距离为![]() ,求△AOB面积的最大值,并求此时直线l的方程.
,求△AOB面积的最大值,并求此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2014年3月的“两会”上,李克强总理在政府工作报告中,首次提出“倡导全民阅读”,某学校响应政府倡导,在学生中发起读书热潮.现统计了从2014年下半年以来,学生每半年人均读书量,如下表:
时间 | 2014年下半年 | 2015年上半年 | 2015年下半年 | 2016年上半年 | 2016年下半年 |
时间代号 |
|
|
|
|
|
人均读书量 |
|
|
|
|
|
根据散点图,可以判断出人均读书量![]() 与时间代号
与时间代号![]() 具有线性相关关系.
具有线性相关关系.
(1)求![]() 关于
关于![]() 的回归方程
的回归方程![]() ;
;
(2)根据所求的回归方程,预测该校2017年上半年的人均读书量.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
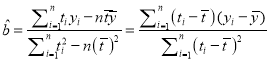 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为2,过右焦点和短轴一个端点的直线的斜率为
的焦距为2,过右焦点和短轴一个端点的直线的斜率为![]() ,
,![]() 为坐标原点.
为坐标原点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,记
两点,记![]() 面积的最大值为
面积的最大值为![]() ,证明:
,证明: ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com