
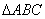 中,
中,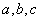 分别是角
分别是角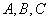 的对边,
的对边,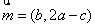 ,
,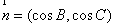 ,且
,且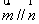
(1)求角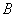 的大小;
的大小;
(2)设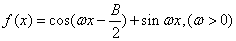 ,且
,且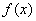 的最小正周期为
的最小正周期为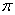 ,求
,求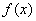 在
在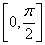 上的最大值和最小值,及相应的
上的最大值和最小值,及相应的 的值。
的值。
(1)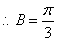
(2)x=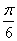 时,f(x)取得最大值
时,f(x)取得最大值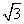 ;x=
;x=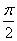 时,f(x)取得最小值-
时,f(x)取得最小值-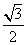 .
.
【解析】
试题分析:(1)由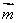 ∥
∥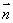 得
得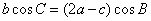 ,
,
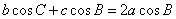
得到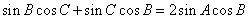 ,
,
所以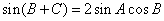 ,又
,又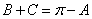 ,所以
,所以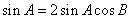
又 ,又
,又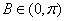 ,
,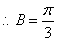
(2) (2)由题知f(x)=cos(ωx-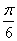 )+sinωx
)+sinωx
=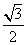 cosωx+
cosωx+ sinωx=
sinωx=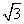 sin(ωx+
sin(ωx+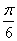 ),
),
由已知得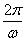 =π,∴ω=2,f(x)=
=π,∴ω=2,f(x)=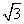 sin(2x+
sin(2x+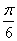 ),
),
当x∈[0,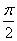 ]时,(2x+
]时,(2x+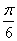 )∈[
)∈[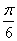 ,
,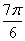 ],
],
sin(2x+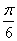 )∈[-
)∈[-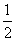 ,1].
,1].
因此,当2x+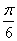 =
= ,即x=
,即x=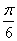 时,f(x)取得最大值
时,f(x)取得最大值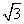 .
.
当2x+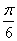 =
=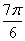 ,即x=
,即x=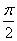 时,f(x)取得最小值-
时,f(x)取得最小值-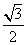 .
.
考点:向量共线,三角函数的性质
点评:主要是考查了三角函数的性质以及解三角形中正弦定理的运用,属于中档题。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
(09年湖北五市联考理)(12分)
已知![]()
![]() ,
,![]()
![]() ,其中
,其中![]() ,若函数
,若函数![]()
![]() ,且
,且![]() 的对称中心到
的对称中心到![]() 对称轴的最近距离不小于
对称轴的最近距离不小于![]()
(Ⅰ)求![]() 的取值范围;
的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分13分)
已知![]()
![]() ,
,![]()
![]() ,其中
,其中![]() ,若函数
,若函数![]()
![]() ,且
,且![]() 的对称中心到
的对称中心到![]() 对称轴的最近距离不小于
对称轴的最近距离不小于![]() (Ⅰ)求
(Ⅰ)求![]() 的取值范围;(Ⅱ)在
的取值范围;(Ⅱ)在![]() 中,
中,![]() 分别是角
分别是角![]() 的对边,且
的对边,且![]() ,当
,当![]() 取最大值时,
取最大值时,![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河南省南阳市高三第八次周考理科数学试卷(解析版) 题型:解答题
(本小题满分12分)
已知向量 ,设函数
,设函数 ,(Ⅰ)求函数
,(Ⅰ)求函数 的表达式;(Ⅱ)在
的表达式;(Ⅱ)在 中,
中, 分别是角
分别是角 的对边,
的对边, 为锐角,若
为锐角,若
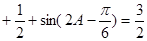 ,
,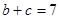 ,
, 的面积为
的面积为 ,求边
,求边 的长.
的长.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河北省石家庄市高三暑期第二次考试理科数学试卷(解析版) 题型:解答题
(本题满分12分)设函数 ,其中向量
,其中向量
 ,
,
向量
 .
.
(1)求 的最小正周期;
的最小正周期;
(2)在 中,
中, 分别是角
分别是角 的对边,
的对边, ,
,
求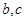 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com