
【题目】如图,已知四边形![]() 为直角梯形,
为直角梯形, ![]() ,若
,若![]() 是以
是以![]() 为底边的等腰直角三角形,且
为底边的等腰直角三角形,且![]() .
.

(1)证明: ![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成的角的大小.
所成的角的大小.
【答案】(1)见解析;(2) ![]() .
.
【解析】试题分析:
(1)要证![]() 与平面
与平面![]() 垂直,就要证
垂直,就要证![]() 与平面
与平面![]() 内两条相交直线垂直,由已知
内两条相交直线垂直,由已知![]() 与
与![]() 垂直,则有
垂直,则有![]() 与平面
与平面![]() 垂直,从而
垂直,从而![]() ,另外在可计算出
,另外在可计算出![]() 的三边长,由勾股定理逆定理可得
的三边长,由勾股定理逆定理可得![]() ,从而证得
,从而证得![]() 平面
平面![]() ;(2)由(1)知
;(2)由(1)知![]() 两两垂直,因此以他们为
两两垂直,因此以他们为![]() 轴建立空间直角坐标系,写出各点坐标,求出平面
轴建立空间直角坐标系,写出各点坐标,求出平面![]() 的法向量与直线
的法向量与直线![]() 的方向向量,由这两个向量夹角与直线与平面所成角的关系可得.
的方向向量,由这两个向量夹角与直线与平面所成角的关系可得.
试题解析:
证明:由已知得: ![]() ,所以
,所以![]() ,即
,即![]()
在直角梯形ABCD中, ![]() ,
, ![]()
![]() ,由
,由![]() 是以
是以![]() 为底边的等腰直角三角形得:
为底边的等腰直角三角形得: ![]()
由![]() ,得
,得![]() ,
,
可算得: ![]()
所以: ![]() ,即PC⊥平面PAD.
,即PC⊥平面PAD.
(2)如图建系,可得:
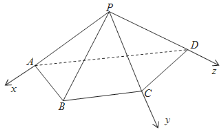
![]() ,
, 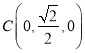 ,
, ![]() ,
, ![]()
![]()
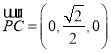 ,
,
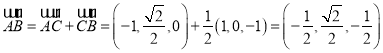 ,
,
设平面PBC的法向量为![]() ,则有
,则有
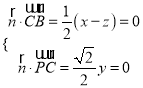 ,令
,令![]() 得:
得: ![]() ,
,
设直线AB与平面PBC所成的角是![]() ,
,
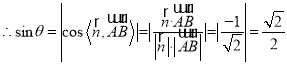
所以直线AB与平面PBC所成的角是![]() .
.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的首项为a,公差为b,方程ax2-3x+2=0的解为1和b,
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=an·2n,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知圆![]() 的圆心在直线
的圆心在直线![]() 上,且过点
上,且过点![]() ,与直线
,与直线![]() 相切.
相切.
(![]() )求圆
)求圆![]() 的方程.
的方程.
(![]() )设直线
)设直线![]() 与圆
与圆![]() 相交于
相交于![]() ,
,![]() 两点.求实数
两点.求实数![]() 的取值范围.
的取值范围.
(![]() )在(
)在(![]() )的条件下,是否存在实数
)的条件下,是否存在实数![]() ,使得弦
,使得弦![]() 的垂直平分线
的垂直平分线![]() 过点
过点![]() ,若存在,求出实数
,若存在,求出实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校准备组织师生共60人,从南靖乘动车前往厦门参加夏令营活动,动车票价格如表所示:(教师按成人票价购买,学生按学生票价购买).
运行区间 | 成人票价(元/张) | 学生票价(元/张) | ||
出发站 | 终点站 | 一等座 | 二等座 | 二等座 |
南靖 | 厦门 | 26 | 22 | 16 |
若师生均购买二等座票,则共需1020元.
(1)参加活动的教师有人,学生有人;
(2)由于部分教师需提早前往做准备工作,这部分教师均购买一等座票,而后续前往的教师和学生均购买二等座票.设提早前往的教师有x人,购买一、二等座票全部费用为y元.
①求y关于x的函数关系式;
②若购买一、二等座票全部费用不多于1032元,则提早前往的教师最多只能多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将一枚质地均匀且四个面上分别标有1,2,3,4的正四面体先后抛掷两次,其底面落于桌面上,记第一次朝下面的数字为![]() ,第二次朝下面的数字为
,第二次朝下面的数字为![]() .用
.用![]() 表示一个基本事件.
表示一个基本事件.
请写出所有基本事件;
求满足条件“![]() ”为整数的事件的概率;
”为整数的事件的概率;
求满足条件“![]() ”的事件的概率.
”的事件的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥S-ABCD中,底面ABCD为菱形,SD⊥平面ABCD,点E为SD的中点.
(1)求证:直线SB∥平面ACE
(2)求证:直线AC⊥平面SBD.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,AD的中点,连接BM,MN,BN.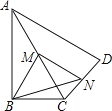
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com