
【题目】已知函数![]()
(Ⅰ)当![]() 时,
时, ![]() 取得极值,求
取得极值,求![]() 的值;
的值;
(Ⅱ)当函数![]() 有两个极值点
有两个极值点![]() ,且
,且![]() 时,总有
时,总有![]()
![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】试题分析:⑴求导后,代入![]() ,
, ![]() 取得极值,从而计算出
取得极值,从而计算出![]() 的值,并进行验证(2)由函数
的值,并进行验证(2)由函数![]() 有两个极值点算出
有两个极值点算出![]() ,继而算出
,继而算出![]() ,不等式转化为
,不等式转化为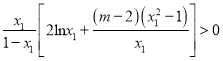 ,构造新函数
,构造新函数![]() ,分类讨论
,分类讨论![]() 、
、![]() 、
、![]() 时三种情况,从而计算出结果
时三种情况,从而计算出结果
解析:(Ⅰ) ![]() ,
, ![]() ,则
,则![]()
检验![]() 时,
时, ![]() ,
,
所以![]() 时,
时, ![]() ,
, ![]() 为增函数;
为增函数;
![]() 时,
时, ![]() ,
, ![]() 为减函数,所以
为减函数,所以![]() 为极大值点
为极大值点
(Ⅱ)![]() 定义域为
定义域为![]() ,有两个极值点
,有两个极值点![]() ,则
,则![]() 在
在![]() 上有两个不等正根
上有两个不等正根
所以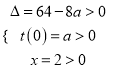 ,所以
,所以![]()
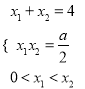 .所以
.所以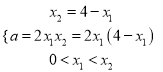 ,所以
,所以![]()
这样原问题即![]() 且
且![]() 时,
时, ![]() 成立
成立
即![]()
即![]()
即![]() ,即
,即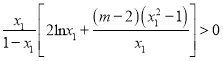
且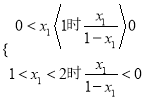
设![]()
![]()
①![]() 时,
时, ![]() ,
,
所以![]() 在
在![]() 上为增函数且
上为增函数且![]() ,
,
所以, ![]() 时,
时, ![]() 不合题意舍去.
不合题意舍去.
②![]() 时,
时, ![]() 同①舍去
同①舍去
③![]() 时
时
(ⅰ)![]() ,即
,即![]() 时可知
时可知![]() ,在
,在![]() 上
上![]() 为减函数且
为减函数且![]() ,
,
这样![]() 时,
时, ![]() ,
, ![]() 时
时![]() ,
,
这样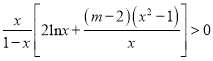 成立
成立
(ⅱ)![]() ,即
,即![]() 时
时![]() 分子中的一元二次函数的对称轴
分子中的一元二次函数的对称轴![]() 开口向下,且1的函数值为
开口向下,且1的函数值为![]()
令![]() ,则
,则![]() 时,
时, ![]() ,
, ![]() 为增函数,
为增函数, ![]()
所以, ![]() 故舍去
故舍去
综上可知: ![]()


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】为了解某工厂![]() 和
和![]() 两车间工人掌握某技术情况,现从这两车间工人中分别抽查
两车间工人掌握某技术情况,现从这两车间工人中分别抽查![]() 名和
名和![]() 名工人,经测试,将这
名工人,经测试,将这![]() 名工人的测试成绩编成的茎叶图。若成绩在
名工人的测试成绩编成的茎叶图。若成绩在![]() 以上(包括
以上(包括![]() )定义为“良好”,成绩在
)定义为“良好”,成绩在![]() 以下定义为“合格”。已知
以下定义为“合格”。已知![]() 车间工人的成绩的平均数为
车间工人的成绩的平均数为![]() ,
,![]() 车间工人的成绩的中位数为
车间工人的成绩的中位数为![]() .
.

(1)求![]() ,
,![]() 的值;
的值;
(2)求![]() 车间工人的成绩的方差;
车间工人的成绩的方差;
(3)在这![]() 名工人中,用分层抽样的方法从 “良好”和“及格”中抽取
名工人中,用分层抽样的方法从 “良好”和“及格”中抽取![]() 人,再从这
人,再从这![]() 人中选
人中选![]() 人,求至少有一人为“良好”的概率。
人,求至少有一人为“良好”的概率。
(参考公式:方差![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义[x]表示不超过的最大整数,如[2]=2,[2,2]=2,执行如图所示的程序框图,则输出S=( ) 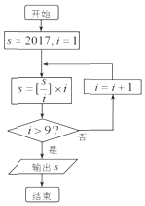
A.1991
B.2000
C.2007
D.2008
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线y2=2px(p>0)的焦点F的直线l与抛物线交于B,C两点,l与抛物线的准线交于点A,且|AF|=6,![]() =2
=2![]() ,
,
(1)求抛物线方程.
(2)求|BC|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=8a2lnx+x2+6ax+b(a,b∈R)
(1)若曲线y=f(x)在点(1,f(1))处的切线方程为y=2x,求a,b的值;
(2)若a≥1,证明:x1 , x2∈(0,+∞),且x1≠x2 , 都有 ![]() >14成立.
>14成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生对其亲属30人的饮食习惯进行了一次调查,并用下图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主)
(1)根据以上数据完成下面的2×2列联表:
主食 蔬菜 | 主食 肉类 | 总计 | |
50岁以下 | |||
50岁以上 | |||
总计 |
(2)能否在犯错误的概率不超过0.010的前提下认为“其亲属的饮食习惯与年龄有关”?并写出简要分析.
附参考公式:![]()
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=( ![]() )ax , a为常数,且函数的图象过点(﹣1,2).
)ax , a为常数,且函数的图象过点(﹣1,2).
(1)求a的值;
(2)若g(x)=4﹣x﹣2,且g(x)=f(x),求满足条件的x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com