
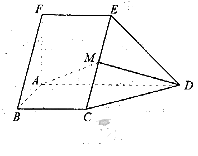
如图,在五面体ABCDEF中,FA 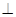 平面ABCD, AD//BC//FE,AB
平面ABCD, AD//BC//FE,AB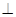 AD,M为EC的中点,AF=AB=BC=FE=
AD,M为EC的中点,AF=AB=BC=FE=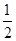 AD
AD
(1)求异面直线BF与DE所成的角的大小;
(2)证明平面AMD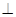 平面CDE;
平面CDE;
(3)求二面角A-CD-E的余弦值.
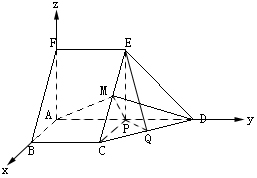
(1)BC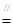 FE ……………………1分
FE ……………………1分
∴BCEF是□ ∴BF//CE
∴∠CED或其补角为BF与DE所成角 ……………………2分
取AD中点P连结EP和CP
∵FE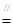 AP ∴FA
AP ∴FA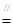 EP
EP
同理AB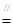 PC 又FA⊥平面ABCD ∴EF⊥平面ABCD
PC 又FA⊥平面ABCD ∴EF⊥平面ABCD
∴EP⊥PC、EP⊥AD 由AB⊥AD PC⊥AD
设FA=a,则EP=PC=PD=a
CD=DE=EC=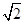 a ∴△ECD是正三角形 ∴∠CED=60o
a ∴△ECD是正三角形 ∴∠CED=60o
∴BF与DE成角60o ……………………2分
(2)∵DC=DE,M为EC中点 ∴DM⊥EC
连结MP,则MP⊥CE 又DM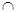 MP=M
MP=M
∴DE⊥平面ADM ……………………3分
又CE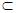 平面CDE ∴平面AMD⊥平面CDE ……
………1分
平面CDE ∴平面AMD⊥平面CDE ……
………1分
(3)取CD中点Q,连结PQ和EQ ∵PC=DQ
∴PQ⊥CD,同理EQ⊥CD ∴∠PQE为二面角的平面角 ……………2分
在Rt△EPQ中,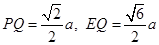
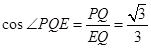
∴二面角A-CD-E的余弦值为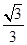
【解析】略


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:高中数学 来源: 题型:
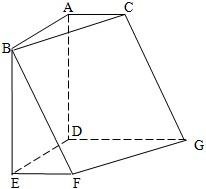 如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,EF∥DG.且AB=AD=DE=DG=2,AC=EF=1.
如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,EF∥DG.且AB=AD=DE=DG=2,AC=EF=1.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在五面体ABCDE中,平面BCD⊥平面ABC,DC=DB=
如图,在五面体ABCDE中,平面BCD⊥平面ABC,DC=DB=| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012年辽宁省鞍山一中高考数学五模试卷(理科)(解析版) 题型:解答题
 ,AC=BC=2ED=2,AC⊥BC,且ED∥AC
,AC=BC=2ED=2,AC⊥BC,且ED∥AC  ,求二面角F-AE-B的余弦值.
,求二面角F-AE-B的余弦值.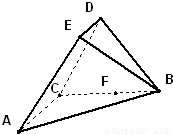
查看答案和解析>>
科目:高中数学 来源:2012年高考数学预测试卷2(文科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com