
【题目】在锐角△ABC中,a,b,c分别为角A,B,C的对边,且4sin2 ![]() ﹣cos2A=
﹣cos2A= ![]() .
.
(1)求角A的大小;
(2)若BC边上高为1,求△ABC面积的最小值?
【答案】
(1)解:∵A+B+C=π,
∴sin ![]() =sin
=sin ![]() =cos
=cos ![]() ,
,
∵4sin2 ![]() ﹣cos2A=
﹣cos2A= ![]() .
.
∴4cos2 ![]() ﹣cos2A=
﹣cos2A= ![]() .
.
∴2(1+cosA)﹣(2cos2A﹣1)= ![]() ,
,
整理得(2cosA﹣1)2=0,
∴cosA= ![]() ,
,
∵0<A<π,
∴A= ![]() .
.
(2)解:过点A作AD⊥BC,在Rt△ABD,Rt△ACD中,sinB= ![]() ,sinC=
,sinC= ![]() ,
,
S△ABC= ![]() bcsinA=
bcsinA= ![]() ×
× ![]() ×
× ![]() ×
× ![]() =
= ![]() ,
,
设y=4sinBsinC,
则y=4sinBsin( ![]() ﹣B)=2
﹣B)=2 ![]() sinBcosB+2sin2B=
sinBcosB+2sin2B= ![]() sin2B+1﹣cos2B=2sin(2B﹣
sin2B+1﹣cos2B=2sin(2B﹣ ![]() )+1,
)+1,
∵0<B< ![]() ,0<
,0< ![]() <
< ![]() ,
,
∴ ![]() <B<
<B< ![]() ,
, ![]() <2B﹣
<2B﹣ ![]() <
< ![]() ,
,
∴当2B﹣ ![]() =
= ![]() ,即B=
,即B= ![]() 时,y有最大值为3,
时,y有最大值为3,
∴此时S有最小值,为 ![]() .
.
【解析】(1)利用三角形内角和,转化B+C,用诱导公式、降幂公式、倍角公式化简,得到关于cosA的方程,求得cosA,进而求得A.(2)在Rt△ABD,Rt△ACD中,sinB= ![]() ,sinC=
,sinC= ![]() ,代入三角形面积公式,求得面积的最值,只需化简求表达式中分母的最值,将C用B表示,利用两角和公式化简,利用B的范围求得分母的最值,进而求得面积的最值.
,代入三角形面积公式,求得面积的最值,只需化简求表达式中分母的最值,将C用B表示,利用两角和公式化简,利用B的范围求得分母的最值,进而求得面积的最值.
【考点精析】掌握三角函数的最值是解答本题的根本,需要知道函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() .
.


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,内角A,B,C所对的边分别为a,b,c,已知 ![]() a=2csinA.
a=2csinA.
(1)求角C的值;
(2)若c= ![]() ,且S△ABC=
,且S△ABC= ![]() ,求a+b的值.
,求a+b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,一个圆柱形乒乓球筒,高为![]() 厘米,底面半径为
厘米,底面半径为![]() 厘米.球筒的上底和下底分别粘有一个乒乓球,乒乓球与球筒底面及侧面均相切(球筒和乒乓球厚度忽略不计).一个平面与两乒乓球均相切,且此平面截球筒边缘所得的图形为一个椭圆,则该椭圆的离心率为( )
厘米.球筒的上底和下底分别粘有一个乒乓球,乒乓球与球筒底面及侧面均相切(球筒和乒乓球厚度忽略不计).一个平面与两乒乓球均相切,且此平面截球筒边缘所得的图形为一个椭圆,则该椭圆的离心率为( )
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,函数y=2sin(πx+φ),x∈R(其中0≤φ≤ ![]() )的图象与y轴交于点(0,1).
)的图象与y轴交于点(0,1). 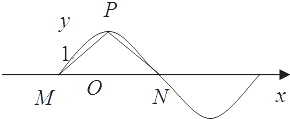
(1)求φ的值.
(2)设P是图象上的最高点,M、N是图象与x轴的交点,求tan∠MPN的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是双曲线
是双曲线![]() 的左右焦点,以
的左右焦点,以![]() 为直径的圆与双曲线的一条渐近线交于点
为直径的圆与双曲线的一条渐近线交于点![]() ,与双曲线交于点
,与双曲线交于点![]() ,且
,且![]() 均在第一象限,当直线
均在第一象限,当直线![]() 时,双曲线的离心率为
时,双曲线的离心率为![]() ,若函数
,若函数![]() ,则
,则![]() ()
()
A. 1 B. ![]() C. 2 D.
C. 2 D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,满足a1=3,a4=12,数列{bn}满足b1=4,b4=20,且{bn﹣an}为等比数列.
(1)求数列{an}和{bn}的通项公式;
(2)求数列{bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,若
,若![]() ,有
,有![]() ,则称函数
,则称函数![]() 为定义在
为定义在![]() 上的非严格单增函数;若
上的非严格单增函数;若![]() ,有
,有![]() ,则称函数
,则称函数![]() 为定义在
为定义在![]() 上的非严格单减函数.
上的非严格单减函数. ![]() .
.
(1)若函数![]() 为定义在
为定义在![]() 上的非严格单增函数,求实数
上的非严格单增函数,求实数![]() 的取值范围.
的取值范围.
(2)若函数![]() 为定义在
为定义在![]() 上的非严格单减函数,试解不等式
上的非严格单减函数,试解不等式![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆![]() 满足:(1)截
满足:(1)截![]() 轴所得弦长为2;(2)被
轴所得弦长为2;(2)被![]() 轴分成两段圆弧,其弧长的比为
轴分成两段圆弧,其弧长的比为![]() .在满足条件(1)、(2)的所有圆中,圆心到直线
.在满足条件(1)、(2)的所有圆中,圆心到直线![]() 的距离最小的圆的方程为__________.
的距离最小的圆的方程为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com