
已知二次函数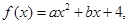 集合
集合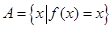
(1)若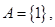 求函数
求函数 的解析式;
的解析式;
(2)若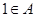 ,且
,且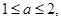 设
设 在区间
在区间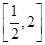 上的最大值、最小值分别为
上的最大值、最小值分别为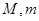 ,记
,记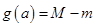 ,求
,求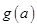 的最小值.
的最小值.
 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:高中数学 来源: 题型:解答题
某产品生产厂家根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品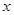 (百台),其总成本为
(百台),其总成本为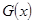 (万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本)。销售收入
(万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本)。销售收入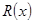 (万元)满足
(万元)满足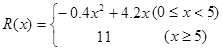 ,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
分别写出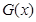 和利润函数
和利润函数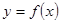 的解析式(利润=销售收入—总成本);
的解析式(利润=销售收入—总成本);
工厂生产多少台产品时,可使盈利最多?并求出此时每台产品的售价。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某医药研究所开发一种新药,据监测,如果成人按规定剂量服用该药,服药后每毫升血液中的含药量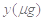 与服药后的时间
与服药后的时间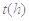 之间近似满足如图所示的曲线.其中
之间近似满足如图所示的曲线.其中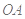 是线段,曲线段
是线段,曲线段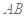 是函数
是函数
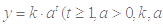 是常数
是常数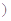 的图象.
的图象.
(1)写出服药后每毫升血液中含药量 关于时间
关于时间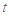 的函数关系式;
的函数关系式;
(2)据测定:每毫升血液中含药量不少于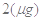 时治疗有效,假若某病人第一次服药为早上
时治疗有效,假若某病人第一次服药为早上 ,为保持疗效,第二次服药最迟是当天几点钟?
,为保持疗效,第二次服药最迟是当天几点钟?
(3)若按(2)中的最迟时间服用第二次药,则第二次服药后再过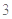
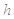 ,该病人每毫升血液中含药量为多少
,该病人每毫升血液中含药量为多少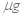 ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某商品在近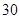 天内每件的销售价格
天内每件的销售价格 (元)与时间
(元)与时间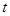 (天)的函数关系是
(天)的函数关系是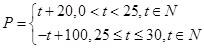 该商品的日销售量
该商品的日销售量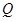 (件)与时间
(件)与时间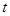 (天)的函数关系是
(天)的函数关系是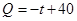
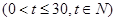 ,设商品的日销售额为
,设商品的日销售额为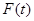 (销售量与价格之积)
(销售量与价格之积)
(1)求商品的日销售额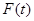 的解析式;
的解析式;
(2)求商品的日销售额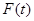 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知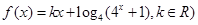 是偶函数.
是偶函数.
(1)求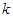 的值;
的值;
(2)证明:对任意实数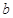 ,函数
,函数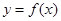 的图像与直线
的图像与直线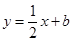 最多只有一个交点;
最多只有一个交点;
(3)设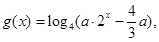 若函数
若函数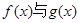 的图像有且只有一个公共点,求实数
的图像有且只有一个公共点,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数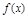 =x2-4x+a+3,g(x)=mx+5-2m.
=x2-4x+a+3,g(x)=mx+5-2m.
(Ⅰ)若方程f(x)=0在[-1,1]上有实数根,求实数a的取值范围;
(Ⅱ)当a=0时,若对任意的x1∈[1,4],总存在x2∈[1,4],使f(x1)=g(x2)成立,求实数m的取值范围;
(Ⅲ)若函数y=f(x)(x∈[t,4])的值域为区间D,是否存在常数t,使区间D的长度为7-2t?若存在,求出t的值;若不存在,请说明理由(注:区间[p,q]的长度为q-p).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com