练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    若函数f（x）=x3+2x2+3ax+4a有一个极大值和一个极小值，则a的取值范围是    ．
    【答案】分析：先求导函数，将函数f（x）=x3+2x2+3ax+4a有一个极大值和一个极小值，转化为方程f′（x）=0有两个不相等的实数根，即可求得的取值范围
    解答：解：求导函数得：f′（x）=3x2+4x+3a
    要使函数f（x）=x3+2x2+3ax+4a有一个极大值和一个极小值，则方程f′（x）=0有两个不相等的实数根
    ∴△=16-36a＞0
    ∴
    ∴a的取值范围是
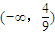
    故答案为：
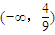    点评：本题以函数为载体，考查导数的运用，考查函数的极值，同时考查了学生分析解决问题的能力，解题的关键是转化为方程f′（x）=0有两个不相等的实数根
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    若函数f（x）=x3+
    1
    x
    ，则
     
    lim
    △x→0
    f(△x-1)+f(1)
    2△x
    等于（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若函数f（x）=x3+3x-1，x∈[-1，l]，则下列判断正确的是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若函数f（x）=x3+3mx2+nx+m2为奇函数，则实数m的值为
    0
    0
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若函数f（x）=x3-3bx+b在区间（0，1）内有极小值，则b的取值范围是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若函数f（x）=x3-3x+1在闭区间[-3，0]上的最大值，最小值分别为M，m，则M+m=
    -14
    -14
    ．

    查看答案和解析>>

    同步练习册答案