
【题目】现有年龄在25到55岁的一群人身体上的某项数据,其频率分布直方图如下.(注:每组包括左端点,不包括右端点)

(1)请补全频率分布直方图;
(2)估计年龄的平均数;(精确到小数点后一位数字)
(3)若50到55岁的人数是50,现在想要从25到35岁的人群中用分层抽样的方法抽取30人,那么25到30岁这一组人中应该抽取多少人?
【答案】(1)见解析;(2)36.8;(3)9人
【解析】
(1)由所有组的频率之和为1可得第二组频率,根据组宽算出组高即可画出;
(2)取各个矩形中间的值为这组的均值计算;
(3)由50到55岁的人数是50,计算出总人数有1000人,再算出25到35岁之间有多少人,根据比例计算即可.
解:(1)第二组的频率为:![]()
所以直方图的高为![]() ,补全的频率分布直方图如图
,补全的频率分布直方图如图
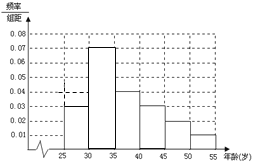
(2)第一组的频率为![]() ,第二组的频率为
,第二组的频率为![]() ,第三组的频率为
,第三组的频率为![]() ,第四组的频率为
,第四组的频率为![]() ,第五组的频率为
,第五组的频率为![]() ,第六组的频率为
,第六组的频率为![]() ,而各组的中点值分别为
,而各组的中点值分别为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,故可估计年龄的平均数为:
,故可估计年龄的平均数为:
![]()
![]()
(3)50到55岁这一组的频率为![]() ,人数是50,故得总人数是
,人数是50,故得总人数是![]()
从而得25到30岁这一组的人数是![]() ,
,
30到35岁这一组的人数是![]()
那么25到30岁这一组人中应该抽取![]() (人)
(人)


科目:高中数学 来源: 题型:
【题目】过圆![]() 上的点
上的点![]() 作圆
作圆![]() 的切线,过点
的切线,过点![]() 作切线的垂线
作切线的垂线![]() ,若直线
,若直线![]() 过抛物线
过抛物线![]() 的焦点
的焦点![]() .
.
(1)求直线![]() 与抛物线
与抛物线![]() 的方程;
的方程;
(2)若直线![]() 与抛物线
与抛物线![]() 交于点
交于点![]() ,点
,点![]() 在抛物线
在抛物线![]() 的准线上,且
的准线上,且![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,其左焦点与抛物线
,其左焦点与抛物线![]() 的焦点重合.
的焦点重合.
(1)求椭圆![]() 的方程;
的方程;
(2)过动点![]() 的直线交
的直线交![]() 轴于点
轴于点![]() ,交椭圆
,交椭圆![]() 于点
于点![]() ,
,![]() 在第一象限,
在第一象限,![]() ,过点
,过点![]() 做
做![]() 轴的垂线交椭圆
轴的垂线交椭圆![]() 于点
于点![]() ,连接
,连接![]() 并延长交椭圆
并延长交椭圆![]() 于另一点
于另一点![]() .设直线
.设直线![]() 的斜率分别为
的斜率分别为![]() ,证明:
,证明:![]() 为定值.
为定值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥PABCD中,AB∥CD ,且∠BAP=∠CDP =90°.
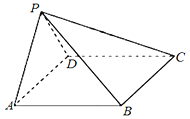
(1).证明:平面PAB⊥平面PAD;
(2).若PA=PD=AB=DC, ∠APD =90°,且四棱锥PABCD的体积为![]() ,求该四棱锥的侧面积.
,求该四棱锥的侧面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正三棱锥P-ABC的侧面是直角三角形,PA=6,顶点P在平面ABC内的正投影为点D,D在平面PAB内的正投影为点E,连结PE并延长交AB于点G.

(Ⅰ)证明:G是AB的中点;
(Ⅱ)在图中作出点E在平面PAC内的正投影F(说明作法及理由),并求四面体PDEF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)的定义域为D={x|x≠0},且满足对于任意x1,x2∈D,有f(x1·x2)=f(x1)+f(x2).
(1)求f(1)的值;
(2)判断f(x)的奇偶性并证明你的结论;
(3)如果f(4)=1,f(x-1)<2,且f(x)在(0,+∞)上是增函数,求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知空间几何体![]() 中,
中, ![]() 与
与![]() 均为边长为2的等边三角形,
均为边长为2的等边三角形, ![]() 为腰长为3的等腰三角形,平面
为腰长为3的等腰三角形,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() .
.
(1)试在平面![]() 内作一条直线,使得直线上任意一点
内作一条直线,使得直线上任意一点![]() 与
与![]() 的连线
的连线![]() 均与平面
均与平面![]() 平行,并给出详细证明;
平行,并给出详细证明;
(2)求三棱锥![]() 的体积.
的体积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位对一岗位面向社会公开招聘,若甲笔试成绩与面试成绩至少有一项比乙高,则称甲不亚于乙.在18位应聘者中,如果某应聘者不亚于其他17人,则称其为“优秀人才”.那么这18人中“优秀人才”数最多为( )
A. 1 B. 2 C. 9 D. 18
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com