
【题目】已知函数![]() .
.
(1)当![]() 时,判断
时,判断![]() 在
在![]() 上的单调性并加以证明;
上的单调性并加以证明;
(2)若![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() 在
在![]() 为增函数;证明见解析(2)
为增函数;证明见解析(2)![]()
【解析】
(1)令![]() ,求出
,求出![]() ,可推得
,可推得![]() ,故
,故![]() 在
在![]() 为增函数;
为增函数;
(2)令![]() ,则
,则![]() ,由此利用分类讨论思想和导数性质求出实数
,由此利用分类讨论思想和导数性质求出实数![]() 的取值范围.
的取值范围.
(1)当![]() 时,
时,![]() .
.
记![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() .
.
所以![]() ,所以
,所以![]() 在
在![]() 单调递增,所以
单调递增,所以![]() .
.
因为![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 为增函数.
为增函数.
(2)由题意,得![]() ,记
,记![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,所以
,所以![]() ,
,
所以![]() 在
在![]() 为增函数,即
为增函数,即![]() 在
在![]() 单调递增,
单调递增,
所以![]() .
.
①当![]() ,
,![]() ,
,![]() 恒成立,所以
恒成立,所以![]() 为增函数,即
为增函数,即![]() 在
在![]() 单调递增,
单调递增,
又![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 为增函数,所以
为增函数,所以![]()
所以![]() 满足题意.
满足题意.
②当![]() ,
,![]() ,令
,令![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,故
,故![]() 在
在![]() 单调递增,
单调递增,
故![]() ,即
,即![]() .
.
故![]() ,
,
又![]() 在
在![]() 单调递增,
单调递增,
由零点存在性定理知,存在唯一实数![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递减,即
单调递减,即![]() 单调递减,
单调递减,
所以![]() ,此时
,此时![]() 在
在![]() 为减函数,
为减函数,
所以![]() ,不合题意,应舍去.
,不合题意,应舍去.
综上所述,![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 中,侧面
中,侧面![]() 底面
底面![]() ,
,![]() 是边长为2的正三角形,已知
是边长为2的正三角形,已知![]() 点满足
点满足![]() .
.
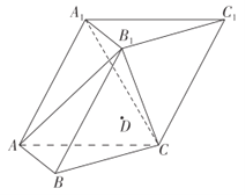
(1)求二面角![]() 的大小;
的大小;
(2)求异面直线![]() 与
与![]() 的距离;
的距离;
(3)直线![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面?若存在,请确定点
平面?若存在,请确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.命题“![]() ”的否定是“
”的否定是“![]() ”
”
B.命题“已知![]() ,若
,若![]() 则
则![]() 或
或![]() ”是真命题
”是真命题
C.命题“若![]() 则函数
则函数![]() 只有一个零点”的逆命题为真命题
只有一个零点”的逆命题为真命题
D.“![]() 在
在![]() 上恒成立”
上恒成立”![]() 在
在![]() 上恒成立
上恒成立
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲,乙两人进行射击比赛,各射击![]() 局,每局射击
局,每局射击![]() 次,射击中目标得
次,射击中目标得![]() 分,未命中目标得
分,未命中目标得![]() 分,两人
分,两人![]() 局的得分情况如下:
局的得分情况如下:
甲 |
|
|
|
|
乙 |
|
|
|
|
(1)若从甲的![]() 局比赛中,随机选取
局比赛中,随机选取![]() 局,求这
局,求这![]() 局的得分恰好相等的概率;
局的得分恰好相等的概率;
(2)从甲,乙两人的![]() 局比赛中随机各选取
局比赛中随机各选取![]() 局,记这
局,记这![]() 局的得分和为
局的得分和为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和为Sn,若对任意正整数n,总存在正整数m,使得Sn=am,则称数列{an}为S数列.
(1)S数列的任意一项是否可以写成其某两项的差?请说明理由.
(2)①是否存在等差数列为S数列,若存在,请举例说明;若不存在,请说明理由.
②是否存在正项递增等比数列为S数列,若存在,请举例说明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个几何体的三视图如图所示,正视图为等腰直角三角形,俯视图中虚线平分矩形的面积,则该几何体的体积为_____,其外接球的表面积为______.
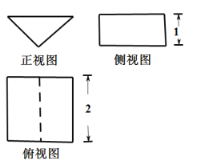
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com