Question

【题目】已知函数.

(1)利用“五点法”画出函数在一个周期上的简图；

(2)先把的图象上所有点向左平移个单位长度，得到的图象；然后把的图

象上所有点的横坐标伸长到原来的2倍(纵坐标不变)，得到的图象；再把的图象

上所有点的纵坐标缩短到原来的倍(横坐标不变)，得到的图象，求的解析式.

Answer 1

【答案】解：(1)见解析， (2).

【解析】

(1) 利用描点法画函数图象，第一步列表，令函数解析式中的角分别为0，，π，，2π，求出x的值，且代入函数解析式求出对应的函数值y的值，找出函数图象上五点坐标，在平面直角坐标系中描出五个点，用平滑的曲线画出函数图象即可；

(2) 利用函数y＝Asin（ωx+φ）的图象变换规律，得出结论.

（1）由“五点作图法”列表如下：

x
x	0		π		2π
3sin（x）	0	3	0	﹣3	0

图象如下：

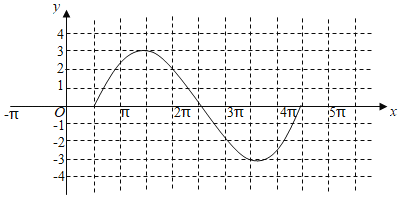
（2）把的图象上所有点向左平移个单位长度，

得到，

把的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)，得到，

把的图象上所有点的纵坐标缩短到原来的倍(横坐标不变)，得到，

∴