练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知椭圆的两个焦点是， ，且椭圆经过点.

    （1）求椭圆的标准方程；

    （2）若过椭圆的左焦点且斜率为1的直线与椭圆交于两点，求线段的长.

    【答案】（1）；（2）.

    【解析】试题分析：（1）椭圆的两个焦点是， ，可得 ，椭圆经过点可得 ，从而可得椭圆的标准方程；（2）直线的方程为，

    代入方程并整理，得，利用韦达定理和弦长公式计算弦长.

    试题解析：（1）由已知得，椭圆的焦点在轴上.

    可设椭圆的方程为，

    点是椭圆短轴的一个顶点，可得，

    由题意可知，则有，

    故椭圆的标准方程为.

    （2）由已知得，直线的方程为，

    代入方程并整理，得.

    设，则，

    则

    .

    【方法点晴】本题主要考查待定系数求椭圆方程以、韦达定理及弦长公式，属于难题.用待定系数法求椭圆方程的一般步骤；①作判断：根据条件判断椭圆的焦点在轴上，还是在轴上，还是两个坐标轴都有可能；②设方程：根据上述判断设方程或 ；③找关系：根据已知条件，建立关于、、的方程组；④得方程：解方程组，将解代入所设方程，即为所求.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知是公差不为零的等差数列，，且，，成等比数列．

    （1）求数列的通项；

    （2）求数列的前项和．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如果定义在（﹣∞，0）∪（0，+∞）上的奇函数f（x），在（0，+∞）内是减函数，又有f（3）=0，则xf（x）＜0的解集为（ ）
    A.{x|﹣3＜x＜0或x＞3}
    B.{x|x＜﹣3或0＜x＜3}
    C.{x|﹣3＜x＜0或0＜x＜3}
    D.{x|x＜﹣3或x＞3}

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为迎接2017年“双”，“双”购物狂欢节的来临，某青花瓷生产厂家计划每天生产汤碗、花瓶、茶杯这三种瓷器共个，生产一个汤碗需分钟，生产一个花瓶需分钟，生产一个茶杯需分钟，已知总生产时间不超过小时．若生产一个汤碗可获利润元，生产一个花瓶可获利润元，生产一个茶杯可获利润元．

    （1）使用每天生产的汤碗个数与花瓶个数表示每天的利润（元）；

    （2）怎样分配生产任务才能使每天的利润最大，最大利润是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了调查中小学课外使用互联网的情况，教育部向华东、华北、华南和西部地区60所中小学发出问卷份， 名学生参加了问卷调查，并根据所得数据画出样本的频率分布直方图（如图）.

    （1）要从这名中小学中用分层抽样的方法抽取名中小学生进一步调查，则在（小时）时间段内应抽出的人数是多少？

    （2）若希望的中小学生每天使用互联网时间不少于（小时），请估计的值，并说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C： 的离心率为，短轴的一个端点到右焦点的距离为．

    (1)求椭圆C的方程；

    (2)设直线l与椭圆C交于A、B两点，坐标原点O到直线l的距离为，求△AOB面积的最大值，并求此时直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列函数中，是偶函数，且在区间（0，1）上为增函数的是（ ）
    A.y=|x|
    B.y=1﹣x
    C.y=
    D.y=﹣x2+4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

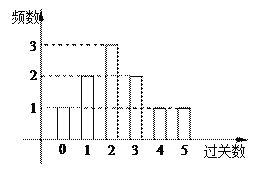
    【题目】某学校在一次第二课堂活动中，特意设置了过关智力游戏，游戏共五关．规定第一关没过者没奖励，过关者奖励件小奖品（奖品都一样）．下图是小明在10次过关游戏中过关数的条形图，以此频率估计概率．

    (Ⅰ)求小明在这十次游戏中所得奖品数的均值；

    (Ⅱ)规定过三关者才能玩另一个高级别的游戏，估计小明一次游戏后能玩另一个游戏的概率；

    (Ⅲ)已知小明在某四次游戏中所过关数为{2,2,3,4}，小聪在某四次游戏中所过关数为{3,3,4,5}，现从中各选一次游戏，求小明和小聪所得奖品总数超过10的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一个几何体的三视图如图所示，其中正视图是一个正三角形，则这个几何体的体积是 ，表面积是 ．

    查看答案和解析>>

    同步练习册答案