
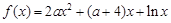 .
.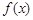 在x=
在x=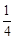 处的切线与直线4x+y=0平行,求a的值;
处的切线与直线4x+y=0平行,求a的值;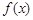 的单调区间;
的单调区间;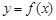 的图象与x轴交于A,B两点,线段AB中点的横坐标为
的图象与x轴交于A,B两点,线段AB中点的横坐标为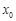 ,证明
,证明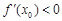 .
.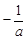 ),单调递减区间为(
),单调递减区间为(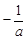 ,+∞);(Ⅲ)详见解析.
,+∞);(Ⅲ)详见解析.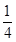 处的切线与直线4x+y=0平行,则
处的切线与直线4x+y=0平行,则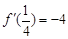 ,求导、代入此式即可得a的值;(Ⅱ)求导得
,求导、代入此式即可得a的值;(Ⅱ)求导得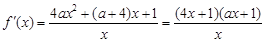 ,由x>0,知
,由x>0,知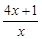 >0,故只需考虑
>0,故只需考虑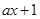 的符号.当a≥0时,对任意x>0,
的符号.当a≥0时,对任意x>0,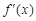 >0恒成立,函数f(x)的单调递增区间为(0,+∞).当a<0时,令
>0恒成立,函数f(x)的单调递增区间为(0,+∞).当a<0时,令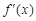 =0,解得
=0,解得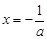 ,由此可得函数f(x)的单调递增区间为(0,
,由此可得函数f(x)的单调递增区间为(0,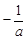 ),单调递减区间为(
),单调递减区间为(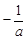 ,+∞);(Ⅲ)因为函数
,+∞);(Ⅲ)因为函数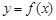 的图象与x轴交于A、B两点,由(Ⅱ)知必有
的图象与x轴交于A、B两点,由(Ⅱ)知必有 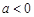 .不妨设A(
.不妨设A(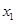 ,0),B(
,0),B(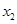 ,0),且
,0),且 ,
, 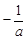 ,+∞)上单调递减,于是要证
,+∞)上单调递减,于是要证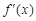 <0成立,只需证:
<0成立,只需证: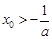 即
即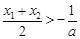 .这个不等式怎么证?这是一个很常见的问题,都是将a换掉,只留
.这个不等式怎么证?这是一个很常见的问题,都是将a换掉,只留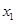 ,
,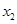 ,然后将这个不等式变形为含
,然后将这个不等式变形为含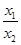 的不等式,然后令
的不等式,然后令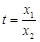 ,再利用导数证明.
,再利用导数证明.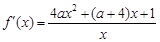 .
.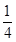 处的切线与直线4x+y=0平行,
处的切线与直线4x+y=0平行,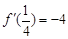 ,
,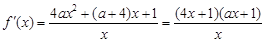 ,
,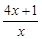 >0.
>0.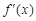 >0,
>0,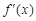 =0,解得
=0,解得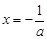 ,
,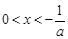 时,
时,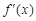 >0,当
>0,当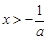 时,
时,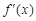 <0,
<0,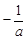 ),单调递减区间为(
),单调递减区间为(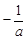 ,+∞). 9分
,+∞). 9分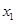 ,0),B(
,0),B(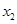 ,0),且
,0),且 ,由(Ⅱ)知
,由(Ⅱ)知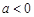 ,
,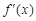 <0成立,只需证:
<0成立,只需证: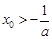 即
即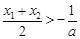 .
.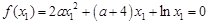 , ①
, ①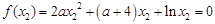 , ②
, ②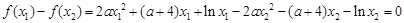 ,
,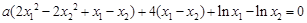 ,
,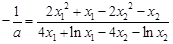 ,
,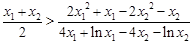 ,
,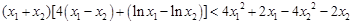 ,
,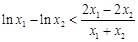 ,变形为
,变形为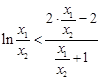 ,
,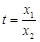
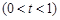 ,令
,令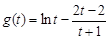 ,
,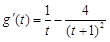
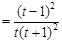 ,
,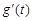 ≥0,当且仅当t=1时,
≥0,当且仅当t=1时,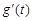 =0,
=0,

科目:高中数学 来源:不详 题型:解答题
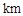 ,货车从甲地匀速行驶到乙地,速度不得超过80
,货车从甲地匀速行驶到乙地,速度不得超过80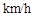 ,已知货车每小时的运输成本(单位:元)由可变成本和固定成本组成,可变成本是速度平方的
,已知货车每小时的运输成本(单位:元)由可变成本和固定成本组成,可变成本是速度平方的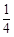 倍,固定成本为a元.
倍,固定成本为a元.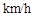 )的函数,并指出这个函数的定义域;
)的函数,并指出这个函数的定义域;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com