
【题目】给出下列五个命题:
①x= ![]() 是函数y=2sin(2x﹣
是函数y=2sin(2x﹣ ![]() )的一条对称轴;
)的一条对称轴;
②函数y=tanx的图象关于点( ![]() ,0)对称;
,0)对称;
③正弦函数在第一象限为增函数
④函数y=cos(x﹣ ![]() )的一个单调增区间是(﹣
)的一个单调增区间是(﹣ ![]() ,
, ![]() )
)
以上四个命题中正确的有(填写正确命题前面的序号)
【答案】①②
【解析】解:①当x= ![]() ,则2×
,则2× ![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]() =
= ![]() ,此时函数y=2sin(2x﹣
,此时函数y=2sin(2x﹣ ![]() )=2sin
)=2sin ![]() =2为函数的最大值,则x=
=2为函数的最大值,则x= ![]() 是函数y=2sin(2x﹣
是函数y=2sin(2x﹣ ![]() )的一条对称轴,正确②函数y=tanx的图象关于点(
)的一条对称轴,正确②函数y=tanx的图象关于点( ![]() ,0)对称,当k=1时,对称中心为(
,0)对称,当k=1时,对称中心为( ![]() ,0)对称;故②正确,③x=
,0)对称;故②正确,③x= ![]() 和x=
和x= ![]() 是第一象限的角,满足
是第一象限的角,满足 ![]() >
> ![]() 但sin
但sin ![]() =sin
=sin ![]() ,则正弦函数在第一象限为增函数,错误,故③错误,④当﹣
,则正弦函数在第一象限为增函数,错误,故③错误,④当﹣ ![]() <x<
<x< ![]() 时,﹣
时,﹣ ![]() <x﹣
<x﹣ ![]() <
< ![]() ,此时函数y=cos(x﹣
,此时函数y=cos(x﹣ ![]() )不单调,故④错误,
)不单调,故④错误,
所以答案是:①②
【考点精析】掌握命题的真假判断与应用是解答本题的根本,需要知道两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:
【题目】我国古代太极图是一种优美的对称图.如果一个函数的图像能够将圆的面积和周长分成两个相等的部分,我们称这样的函数为圆的“太极函数”.下列命题中错误命题的个数是( )
![]() 对于任意一个圆其对应的太极函数不唯一;
对于任意一个圆其对应的太极函数不唯一;
![]() 如果一个函数是两个圆的太极函数,那么这两个圆为同心圆;
如果一个函数是两个圆的太极函数,那么这两个圆为同心圆;
![]() 圆
圆![]() 的一个太极函数为
的一个太极函数为![]() ;
;
![]() 圆的太极函数均是中心对称图形;
圆的太极函数均是中心对称图形;
![]() 奇函数都是太极函数;
奇函数都是太极函数;
![]() 偶函数不可能是太极函数.
偶函数不可能是太极函数.
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某个服装店经营某种服装,在某周内获纯利润y/元与该周每天销售这种服装件数x/件之间的数据如表:
X | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
y | 66 | 69 | 73 | 81 | 89 | 90 | 91 |
已知x12+x22+…+x72=280,x1y1+x2y2+…+x7y7=3487.
(1)求 ![]() ,
, ![]() ;
;
(2)画出散点图;
(3)判断纯利润y与每天销售件数x之间是否线性相关,如果线性相关,求出线性回归方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某中学举行的物理知识竞赛中,将三个年级参赛学生的成绩在进行整理后分成5组,绘制出如图所示的频率分布直方图,图中从左到右依次为第一、第二、第三、第四、第五小组.已知第三小组的频数是15. 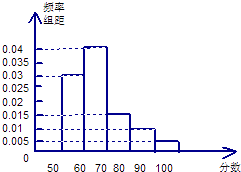
(1)求成绩在50~70分的频率是多少;
(2)求这三个年级参赛学生的总人数是多少;
(3)求成绩在80~100分的学生人数是多少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人上午7时,乘摩托艇以匀速vkm/h(8≤v≤40)从A港出发到距100km的B港去,然后乘汽车以匀速wkm/h(30≤w≤100)自B港向距300km的C市驶去.应该在同一天下午4至9点到达C市. 设乘坐汽车、摩托艇去目的地所需要的时间分别是xh,yh.
(1)作图表示满足上述条件的x,y范围;
(2)如果已知所需的经费p=100+3(5﹣x)+2(8﹣y)(元),那么v,w分别是多少时p最小?此时需花费多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于平面向量 ![]() ,
, ![]() ,
, ![]() ,有下列三个命题:
,有下列三个命题:
①若 ![]()
![]() =
= ![]()
![]() ,则
,则 ![]() =
= ![]() 、
、
②若 ![]() =(1,k),
=(1,k), ![]() =(﹣2,6),
=(﹣2,6), ![]() ∥
∥ ![]() ,则k=﹣3.
,则k=﹣3.
③非零向量 ![]() 和
和 ![]() 满足|
满足| ![]() |=|
|=| ![]() |=|
|=| ![]() ﹣
﹣ ![]() |,则
|,则 ![]() 与
与 ![]() +
+ ![]() 的夹角为60°.
的夹角为60°.
其中真命题的序号为 . (写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一条光线从点(﹣2,﹣3)射出,经y轴反射后与圆(x+3)2+(y﹣2)2=1相切,则反射光线所在直线的斜率为( )
A.﹣ ![]() 或﹣
或﹣ ![]()
B.﹣ ![]() 或﹣
或﹣ ![]()
C.﹣ ![]() 或﹣
或﹣ ![]()
D.﹣ ![]() 或﹣
或﹣ ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com