
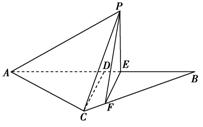
如右图所示,等腰三角形△ABC的底边AB=6,高CD=3,
点E是线段BD上异于B、D的动点,点F在BC边上,且EF⊥AB,现沿EF将△BEF折起到△PEF的位置,使PE⊥AE,记BE=x,V(x)表示四棱锥P-ACEF的体积.
(1)求V(x)的表达式;
 (2)当x为何值时,V(x)取得最大值?
(2)当x为何值时,V(x)取得最大值?
(3)当V(x)取得最大值时,求异面直线AC与PF所成角的余弦值
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com