
【题目】[选修4-4:坐标系与参数方程]
已知极坐标系的极点在直角坐标系的原点处,极轴与![]() 轴的非负半轴重合,直线
轴的非负半轴重合,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)设![]() ,
, ![]() 分别是直线
分别是直线![]() 与曲线
与曲线![]() 上的点,求
上的点,求![]() 的最小值.
的最小值.
科目:高中数学 来源: 题型:
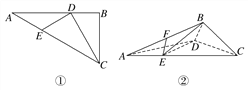
【题目】如图①所示,在Rt△ABC中,AC=6,BC=3,∠ABC=90°,CD为∠ACB的平分线,点E在线段AC上,CE=4,将△BCD沿CD折起,使得平面BCD⊥平面ACD,连接AB,BE,如图②所示,设点F是AB的中点.
(1)求证:DE⊥平面BCD;
(2)若EF∥平面BDG,其中G为AC上一点,求三棱锥B-DEG的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位200名职工的年龄分布情况如图,现要从中抽取40名职工作样本.用系统抽样法,将全体职工随机按1~200编号,并按编号顺序平均分为40组(1~5号,6~10号,…,196~200号).若第5组抽出的号码为22,则第8组抽出的号码应是________.若用分层抽样法,则40岁的以下的年龄段应抽取__________人.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定椭圆![]() ,称圆
,称圆![]() 为椭圆
为椭圆![]() 的“伴随圆”.已知点
的“伴随圆”.已知点![]() 是椭圆
是椭圆![]() 上的点
上的点
(1)若过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点,求
有且只有一个公共点,求![]() 被椭圆
被椭圆![]() 的伴随圆
的伴随圆![]() 所截得的弦长:
所截得的弦长:
(2)![]() 是椭圆
是椭圆![]() 上的两点,设
上的两点,设![]() 是直线
是直线![]() 的斜率,且满足
的斜率,且满足![]() ,试问:直线
,试问:直线![]() 是否过定点,如果过定点,求出定点坐标,如果不过定点,试说明理由。
是否过定点,如果过定点,求出定点坐标,如果不过定点,试说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),将曲线
为参数),将曲线![]() 上各点的横坐标都缩短为原来的
上各点的横坐标都缩短为原来的![]() 倍,纵坐标坐标都伸长为原来的
倍,纵坐标坐标都伸长为原来的![]() 倍,得到曲线
倍,得到曲线![]() ,在极坐标系(与直角坐标系
,在极坐标系(与直角坐标系![]() 取相同的单位长度,且以原点
取相同的单位长度,且以原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴)中,直线
轴非负半轴为极轴)中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 是曲线
是曲线![]() 上的一个动点,求它到直线
上的一个动点,求它到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为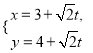 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,并使得它与直角坐标系
轴的正半轴为极轴建立极坐标系,并使得它与直角坐标系![]() 有相同的长度单位,曲线
有相同的长度单位,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 与直线
与直线![]() 交于
交于![]() 、
、![]() 两点,且
两点,且![]() 点的坐标为
点的坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家电公司根据销售区域将销售员分成![]() 两组.2017年年初,公司根据销售员的销售业绩分发年终奖,销售员的销售额(单位:十万元)在区间
两组.2017年年初,公司根据销售员的销售业绩分发年终奖,销售员的销售额(单位:十万元)在区间![]() 内对应的年终奖分别为2万元,2.5万元,3万元,3.5万元.已知200名销售员的年销售额都在区间
内对应的年终奖分别为2万元,2.5万元,3万元,3.5万元.已知200名销售员的年销售额都在区间![]() 内,将这些数据分成4组:
内,将这些数据分成4组: ![]() ,得到如下两个频率分布直方图:
,得到如下两个频率分布直方图:

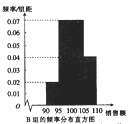
以上面数据的频率作为概率,分别从![]() 组与
组与![]() 组的销售员中随机选取1位,记
组的销售员中随机选取1位,记![]() 分别表示
分别表示![]() 组与
组与![]() 组被选取的销售员获得的年终奖.
组被选取的销售员获得的年终奖.
(1)求![]() 的分布列及数学期;
的分布列及数学期;
(2)试问![]() 组与
组与![]() 组哪个组销售员获得的年终奖的平均值更高?为什么?
组哪个组销售员获得的年终奖的平均值更高?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com