
【题目】如图,在四棱锥![]() 中,四边形
中,四边形![]() 是边长为2的正方形,
是边长为2的正方形,![]() ,
,![]() 为
为![]() 的中点,点
的中点,点![]() 在
在![]() 上,
上,![]() 平面
平面![]() ,
,![]() 在
在![]() 的延长线上,且
的延长线上,且![]() .
.
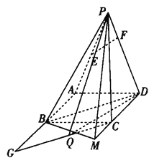
(1)证明:![]() 平面
平面![]() .
.
(2)过点![]() 作
作![]() 的平行线,与直线
的平行线,与直线![]() 相交于点
相交于点![]() ,点
,点![]() 为
为![]() 的中点,求
的中点,求![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)见解析;(2)![]()
【解析】
(1)取![]() 的中点为
的中点为![]() ,连接
,连接![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,通过证明四边形
,通过证明四边形![]() 是平行四边形,得
是平行四边形,得![]() ,证得线面平行;
,证得线面平行;
(2)考虑三棱锥![]() 的体积,利用等体积法求出
的体积,利用等体积法求出![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,![]() 到平面
到平面![]() 的距离是
的距离是![]() 到平面
到平面![]() 的距离的一半,即可得解.
的距离的一半,即可得解.
(1)证明:记![]() 的中点为
的中点为![]() ,连接
,连接![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,
,
则![]() ,且
,且![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
在![]() 中,
中,![]() ,
,![]() ,易求
,易求![]() ,
,![]() .
.
又![]() ,则
,则![]() .
.
因为![]() ,所以
,所以![]() .
.
因为![]() ,且
,且![]() ,所以四边形
,所以四边形![]() 是平行四边形,
是平行四边形,
所以![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
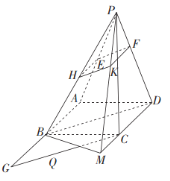
(2)因为![]() 平面
平面![]() ,所以
,所以![]() ,而
,而![]() 是正方形,所以
是正方形,所以![]() .
.
因为![]() 与
与![]() 显然是相交直线,所以
显然是相交直线,所以![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
记![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
,![]() ,则
,则![]() 平面
平面![]() ,且
,且![]() .
.
因为点![]() 为
为![]() 的中点,所以
的中点,所以![]() ,
,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,所以
,所以![]() .
.
![]() ,所以
,所以![]() ,
,
而三棱锥![]() 的体积
的体积![]() .
.
记![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
则![]() ,所以
,所以![]() .
.
因为![]() 到平面
到平面![]() 的距离是
的距离是![]() 到平面
到平面![]() 的距离的一半,
的距离的一半,
所以![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】己知某区甲、乙、丙三所学校的教师志愿者人数分别为240,160,80.为助力疫情防控,现采用分层抽样的方法,从这三所学校的教师志愿者中抽取6名教师,参与“抗击疫情·你我同行”下卡口执勤值守专项行动.
(Ⅰ)求应从甲、乙、丙三所学校的教师志愿者中分别抽取的人数;
(Ⅱ)设抽出的6名教师志愿者分别记为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,现从中随机抽取2名教师志愿者承担测试体温工作.
,现从中随机抽取2名教师志愿者承担测试体温工作.
(i)试用所给字母列举出所有可能的抽取结果;
(ii)设![]() 为事件“抽取的2名教师志愿者来自同一所学校”,求事件
为事件“抽取的2名教师志愿者来自同一所学校”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛掷一个质地均匀的骰子的试验,事件A表示“小于5的偶数点出现”,事件B表示“不小于5的点数出现”,则一次试验中,事件A或事件B至少有一个发生的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,直线
,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,与曲线
,与曲线![]() 相交于点
相交于点![]() ,且
,且![]()
(1)求抛物线![]() 的方程;
的方程;
(2)过抛物线![]() 的焦点
的焦点![]() 的直线
的直线![]() 交抛物线于
交抛物线于![]() 两点,过
两点,过![]() 分别作抛物线的切线,两切线交于点
分别作抛物线的切线,两切线交于点![]() ,求证点
,求证点![]() 的纵坐标为定值.
的纵坐标为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一机器可以按各种不同的速度运转,其生产物件有一些会有缺点,每小时生产有缺点物件的多少随机器运转速度而变化,用x表示转速(单位:转/秒),用y表示每小时生产的有缺点物件个数,现观测得到![]() 的4组观测值为
的4组观测值为![]() .
.
(1)假定y与x之间有线性相关关系,求y对x的回归直线方程.
(2)若实际生产中所容许的每小时最大有缺点物件数为10,则机器的速度不得超过多少转/秒?(精确到1转/秒)
回归直线的斜率和截距的最小二乘估计公式分别为: ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com