
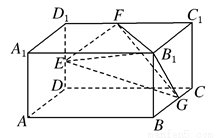
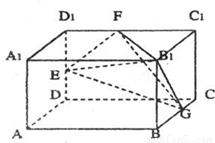
如图,长方体AC1中,AB=2,BC=AA1=1.E、F、G分别为棱DD1、D1C1、BC的中点.
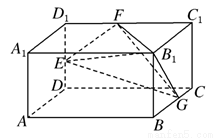
(1)求证:平面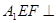 平面
平面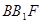 ;
;
(2)在底面A1D1上有一个靠近D1的四等分点H,求证: EH∥平面FGB1;
(3)求四面体EFGB1的体积.
(1)见解析;
(2) H在A1D1上,且HD1=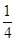 A1D1时,EH∥平面FGB1.
A1D1时,EH∥平面FGB1.
(3) V四面体EFGB1=VE—FGB1=VH—FGB1=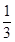 ×1×
×1× =
=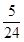 .
.
【解析】
试题分析:(1)根据面面垂直的判定定理来得到证明。
(2)取A1D1的中点P,D1P的中点H,连接DP、EH,通过EH∥平面FGB1,说明EH∥B1G,得到HD1= 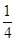 A1D1.
A1D1.
(3)以D为原点,直线DA、DC、DD1为x、y、z轴建立空间直角坐标系,利用法向量,求出E到平面FGB1的距离d,底面S△FGB1,然后求四面体EFGB1的体积.
解:(1)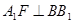
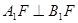

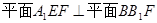
(2)取A1D1的中点P,D1P的中点H,连结DP、EH,则DP∥B1G,EH∥DP,
∴EH∥B1G,又B1G⊂平面FGB1,∴EH∥平面FGB1.
即H在A1D1上,且HD1=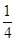 A1D1时,EH∥平面FGB1.
A1D1时,EH∥平面FGB1.
(3)∵EH∥平面FGB1,∴VE—FGB1=VH—FGB1,
而VH—FGB1=VG—HFB1=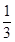 ×1×S△HFB1,
×1×S△HFB1,
S△HFB1=S梯形B1C1D1H-S△B1C1F-S△D1HF= ,
,
∴V四面体EFGB1=VE—FGB1=VH—FGB1=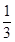 ×1×
×1× =
=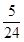 .
.
考点:本题主要考查了考查直线与平面的位置关系,探究点的位置,几何体的体积的求法,考查空间想象能力,计算能力.中档试题。
点评:解决该试题的关键是熟练的利用面面垂直的判定定理得到证明,同时能家里空间直角坐标系来表示平面的法向量,进而求解体积。


科目:高中数学 来源: 题型:
 (2009•湖北模拟)如图,长方体AC1中,AB=2,BC=AA1=1,E、F、G分别为棱DD1、D1C1、BC的中点,
(2009•湖北模拟)如图,长方体AC1中,AB=2,BC=AA1=1,E、F、G分别为棱DD1、D1C1、BC的中点,查看答案和解析>>
科目:高中数学 来源:2014届江西省高二第四次月考文科数学试卷(解析版) 题型:解答题
如图,长方体AC1中,AB=2,BC=AA1=1.E、F、G分别为棱DD1、D1C1、BC的中点.
(1)求证:平面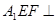 平面
平面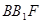 ;
;
(2)在底面A1D1上有一个靠近D1的四等分点H,求证: EH∥平面FGB1;
(3)求四面体EFGB1的体积.
查看答案和解析>>
科目:高中数学 来源:2008-2009学年湖北省百所重点中学高三第二次联考数学试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2011年广东省广州市仲元中学高三数学专题训练:直线、平面、简单几何(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com