
已知函数 的定义域为
的定义域为 ,且同时满足以下三个条件:①
,且同时满足以下三个条件:①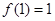 ;②对任意的
;②对任意的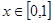 ,都有
,都有 ;③当
;③当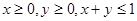 时总有
时总有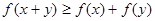 .
.
(1)试求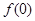 的值;
的值;
(2)求 的最大值;
的最大值;
(3)证明:当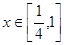 时,恒有
时,恒有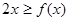 .
.
(1)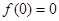 ;(2)
;(2)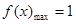 ;(3)
;(3)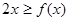 .
.
解析试题分析:(1)抽象函数求在特殊点的值,一般用赋值法,令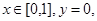 代入抽象函数可得
代入抽象函数可得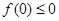 ,又因为
,又因为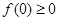 ,可得
,可得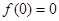 .(2)在定义域内求抽象函数最值,一般先判断函数单调性,再求比较定义域端点的函数值和极值点的大小.证明单调性可令
.(2)在定义域内求抽象函数最值,一般先判断函数单调性,再求比较定义域端点的函数值和极值点的大小.证明单调性可令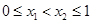 ,代入得
,代入得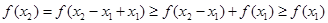 进而得函数为增函数,最大值为
进而得函数为增函数,最大值为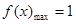 ;
;
(3)在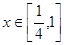 上证不等式
上证不等式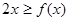 ,要分两段
,要分两段 、
、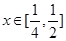 .在
.在 上
上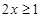 ,
,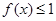 ,所以
,所以 .在
.在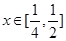
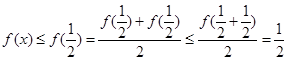 ,
,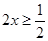 ,所以
,所以 ,进而得证.
,进而得证.
试题解析:(1)令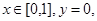 则有
则有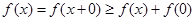 ,所以有
,所以有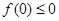 ,有根据条件?可知
,有根据条件?可知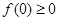 ,故
,故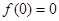 .(也可令
.(也可令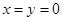 )
)
方法一:设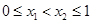 ,则有
,则有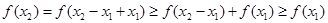 ,即
,即 为增函数(严格来讲为不减函数),所以
为增函数(严格来讲为不减函数),所以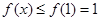 ,故
,故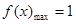 .
.
方法二:不妨令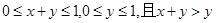 ,所以由?
,所以由?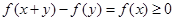 ,即
,即 增函数(严格来讲为不减函数),所以
增函数(严格来讲为不减函数),所以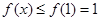 ,故
,故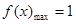 .
.
(3)当 ,有
,有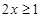 ,又由?可知
,又由?可知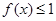 ,所以有
,所以有 对任意的
对任意的 恒成立.当
恒成立.当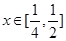 ,又由?可知
,又由?可知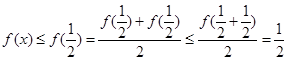 ,所以有
,所以有 对任意的
对任意的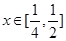 恒成立.综上,对任意的
恒成立.综上,对任意的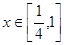 时,恒有
时,恒有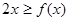 .
.
考点:1.抽象函数求值和单调性;2.证明不等式.


科目:高中数学 来源: 题型:解答题
已知函数 ,点
,点 、
、 在函数
在函数 的图象上,
的图象上,
点 在函数
在函数 的图象上,设
的图象上,设
 .
.
(1)求数列 的通项公式;
的通项公式;
(2)记 ,求数列
,求数列 的前
的前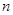 项和为
项和为 ;
;
(3)已知 ,记数列
,记数列 的前
的前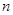 项和为
项和为 ,数列
,数列 的前
的前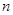 项和为
项和为 ,试比较
,试比较 与
与 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示, 是一个矩形花坛,其中AB= 4米,AD = 3米.现将矩形花坛
是一个矩形花坛,其中AB= 4米,AD = 3米.现将矩形花坛 扩建成一个更大的矩形花园
扩建成一个更大的矩形花园 ,要求:B在
,要求:B在 上,D在
上,D在 上,对角线
上,对角线 过C点, 且矩形
过C点, 且矩形 的面积小于64平方米.
的面积小于64平方米.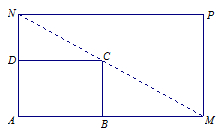
(Ⅰ)设 长为
长为 米,矩形
米,矩形 的面积为
的面积为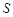 平方米,试用解析式将
平方米,试用解析式将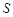 表示成
表示成 的函数,并写出该函数的定义域;
的函数,并写出该函数的定义域;
(Ⅱ)当 的长度是多少时,矩形
的长度是多少时,矩形 的面积最小?并求最小面积.
的面积最小?并求最小面积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某市电力公司在电力供不应求时期,为了居民节约用电,采用“阶梯电价”方法计算电价,每月用电不超过 度时,按每度
度时,按每度 元计费,每月用电超过
元计费,每月用电超过 度时,超过部分按每度
度时,超过部分按每度 元计费,每月用电超过
元计费,每月用电超过 度时,超过部分按每度
度时,超过部分按每度 元计费
元计费
(Ⅰ)设每月用电 度,应交电费
度,应交电费 元,写出
元,写出 关于
关于 的函数;
的函数;
(Ⅱ)已知小王家第一季度缴费情况如下:
| 月份 | 1 | 2 | 3 | 合计 |
| 缴费金额 | 87元 | 62元 | 45元8角 | 194元8角 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)是定义在R上的奇函数,且f(x)的图象关于直线x=1对称.
(1)求证:f(x)是周期为4的周期函数;
(2)若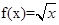 (0<x≤1),求x∈[-5,-4]时,函数f(x)的解析式.
(0<x≤1),求x∈[-5,-4]时,函数f(x)的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
停车场预计“十·一”国庆节这天将停放大小汽车1200辆次,该停车场的收费标准为:大车每辆次10元,小车每辆次5元.根据预计,解答下面的问题:
(1)写出国庆节这天停车场的收费金额y(元)与小车停放辆次x(辆)之间的函数关系式,并指出自变量x的取值范围;
(2)如果国庆节这天停放的小车辆次占停车总辆次的65%~85%,请你估计国庆节这天该停车场收费金额的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com