
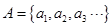 ,定义
,定义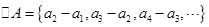 它的第
它的第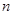 项为
项为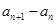
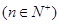 ,假设
,假设 是首项是
是首项是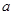 公比为
公比为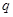 的等比数列.
的等比数列.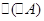 的前
的前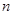 项和
项和 ;
;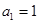 ,
,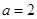 ,
,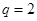 .
.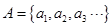 的通项
的通项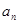 ;
;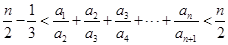 .
.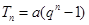 ;(2)①
;(2)①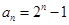 ;②详见解析.
;②详见解析. 是首项是
是首项是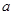 公比为
公比为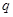 的等比数列,故实数列
的等比数列,故实数列 确定,即
确定,即
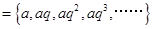 ,再结合
,再结合 的定义,得
的定义,得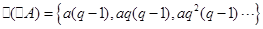 ,然后求和即可(需分类讨论);(2)由
,然后求和即可(需分类讨论);(2)由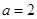 ,
,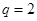 .,可确定
.,可确定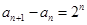 ,利用累加法可求
,利用累加法可求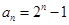 ;和式
;和式 可看作数列
可看作数列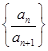 的前n项和,故先求其通项公式,得
的前n项和,故先求其通项公式,得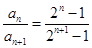 ,因前n项和不易直接求出,故可考虑放缩法,首先看不等式右边,可想到证明每项都小于
,因前n项和不易直接求出,故可考虑放缩法,首先看不等式右边,可想到证明每项都小于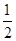 ,由
,由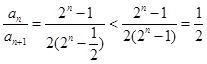 ,进而可证明右面不等式,再考虑不等式左边,
,进而可证明右面不等式,再考虑不等式左边, ,因为
,因为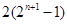
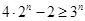 ,故
,故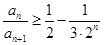 ,进而求和可证明.
,进而求和可证明.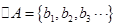 这里
这里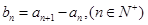

 是公比为
是公比为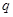 的等比数列.
的等比数列.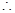
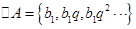
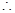
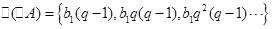 ,
,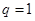 时,
时,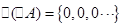 ,
,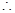
 ,. 2分
,. 2分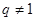 时,
时,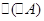 是公比为
是公比为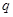 ,首项为
,首项为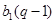 的等比数列;.
的等比数列;.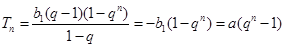 . 4分
. 4分 综上
综上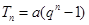
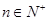 . 6分
. 6分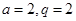 ,
,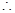
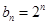 ,
,
 叠加可得
叠加可得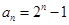 (
(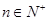 ). 8分
). 8分
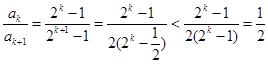
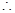
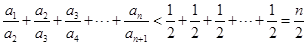 . 10分
. 10分
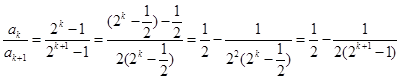
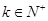 ,
,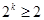 ,
,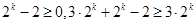
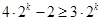 ,
,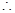
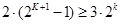 ,
,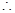

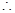
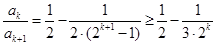 . 12分
. 12分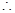
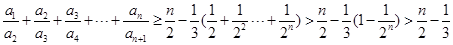
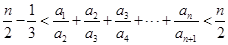 . 13分
. 13分

 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com