已知函数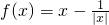 .
.
(I)若f(2x)=2,求x的值;
(II)若tf(t2)+mf(t)≥0对于t∈[2,4]恒成立,求实数m的取值范围.
解:(I)∵2
x>0
∴f(x)=
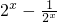
=2
∴2
2x-2•2
x-1=0
∴
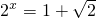
∴
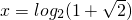
(II)∵t∈[2,4]
∴f(t)=t-

,
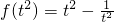
∵tf(t
2)+mf(t)≥0恒成立即
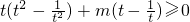
恒成立
∴(t-

)(t
2+1+m)≥0
∵t∈[2,4]
∴
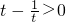
∴t
2+1+m≥0
∴m≥-(t
2+1)恒成立
当t∈[2,4]时,-(1+t
2)∈[-17,-5]
∴m≥-5
分析:(I)由2
x>0,直接代入可求f(x)=
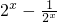
,结合f(x)=2可求2
x,进而可求x
(II)由t∈[2,4]可求f(t),f(t
2),结合tf(t
2)+mf(t)≥0恒成立可得
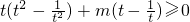
恒成立,结合
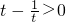
整理可得m≥-(t
2+1)恒成立,从而转化为求解1+t
2)的最大值即可
点评:本题主要考查了指数与对数相互转化的应用及恒成立问题的求解,属于函数知识的简单应用
练习册系列答案
相关习题
科目:高中数学
来源:2011-2012学年安徽省省城名校高三第一次联考数学试卷(理科)(解析版)
题型:解答题
已知函数
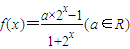
.
(I)若f(x)为奇函数,求a的值;
(III)当a=5时,函数f(x)的图象是否存在对称中心,若存在,求其对称中心;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学
来源:宁夏回族自治区月考题
题型:解答题
已知函数
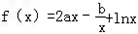
.
(I)若f(x)在

处取和极值,
①求a、b的值;
②存在
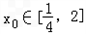
,使得不等式f(
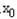
)-c≤0成立,求c的最小值;
(II)当b=a时,若f(x)在(0,+∞)上是单调函数,求a的取值范围
(参考数据e
2≈7.389,e
3≈20.08)
查看答案和解析>>
科目:高中数学
来源:2013年广东省汕头市高考数学一模试卷(理科)(解析版)
题型:解答题
已知函数
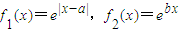
.
(I)若f(x)=f
1(x)+f
2(x)-bf
2(-x),是否存在a,b∈R,y=f(x)为偶函数.如果存在.请举例并证明你的结论,如果不存在,请说明理由;
〔II)若a=2,b=1.求函数g(x)=f
1(x)+f
2(x)在R上的单调区间;
(III )对于给定的实数?x
∈[0,1],对?x∈[0,1],有|f
1(x)-f
2(x
)|<1成立.求a的取值范围.
查看答案和解析>>
科目:高中数学
来源:2010年高考数学预测试卷(押题卷1)(解析版)
题型:解答题
已知函数
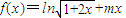
.
(I)若f(x)为定义域上的单调函数,求实数m的取值范围;
(II)当m=1,且1≥a>b≥0时,证明:
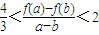
.
查看答案和解析>>
科目:高中数学
来源:2010年四川省攀枝花市高考数学三模试卷(理科)(解析版)
题型:解答题
已知函数
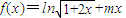
.
(I)若f(x)为定义域上的单调函数,求实数m的取值范围;
(II)当m=1,且1≥a>b≥0时,证明:
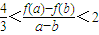
.
查看答案和解析>>

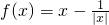 .
.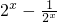 =2
=2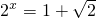
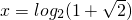
 ,
,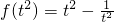
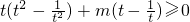 恒成立
恒成立 )(t2+1+m)≥0
)(t2+1+m)≥0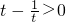
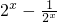 ,结合f(x)=2可求2x,进而可求x
,结合f(x)=2可求2x,进而可求x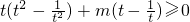 恒成立,结合
恒成立,结合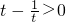 整理可得m≥-(t2+1)恒成立,从而转化为求解1+t2)的最大值即可
整理可得m≥-(t2+1)恒成立,从而转化为求解1+t2)的最大值即可

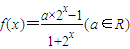 .
.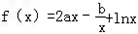 .
. 处取和极值,
处取和极值,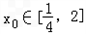 ,使得不等式f(
,使得不等式f(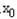 )-c≤0成立,求c的最小值;
)-c≤0成立,求c的最小值;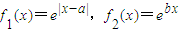 .
.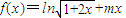 .
.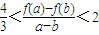 .
.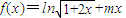 .
.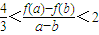 .
.