
【题目】如图, ![]() 是边长为
是边长为 ![]() 的正方形,
的正方形, ![]() 平面
平面 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 与平面
与平面 ![]() 所成角为
所成角为 ![]() .
.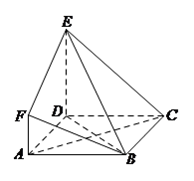
(Ⅰ)求证: ![]() 平面
平面 ![]() .
.
(Ⅱ)求二面角 ![]() 的余弦值.
的余弦值.
(Ⅲ)设点 ![]() 是线段
是线段 ![]() 上一个动点,试确定点
上一个动点,试确定点 ![]() 的位置,使得
的位置,使得 ![]() 平面
平面 ![]() ,并证明你的结论.
,并证明你的结论.
【答案】解:(Ⅰ)证明:∵ ![]() 平面
平面 ![]() ,
, ![]() 平面
平面 ![]() ,
,
∴ ![]() ,
,
又∵ ![]() 是正方形,
是正方形,
∴ ![]() ,
,
∵ ![]() ,
,
∴ ![]() 平面
平面 ![]() .
.
(Ⅱ)解:∵ ![]() ,
, ![]() ,
, ![]() 两两垂直,所以建立如图空间直角坐标系
两两垂直,所以建立如图空间直角坐标系 ![]() ,
,

∵ ![]() 与平面
与平面 ![]() 所成角为
所成角为 ![]() ,即
,即 ![]() ,
,
∴ ![]() ,
,
由 ![]() ,可知:
,可知: ![]() ,
, ![]() .
.
则 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
∴ ![]() ,
, ![]() ,
,
设平面 ![]() 的法向量为
的法向量为 ![]() ,则
,则
 ,即
,即 ![]() ,
,
令 ![]() ,则
,则 ![]() .
.
因为 ![]() 平面
平面 ![]() ,所以
,所以 ![]() 为平面
为平面 ![]() 的法向量,
的法向量,
∴ ![]() ,
,
所以  .
.
因为二面角为锐角,
故二面角 ![]() 的余弦值为
的余弦值为 ![]() .
.
(Ⅲ)解:依题意得,设 ![]() ,
,
则 ![]() ,
,
∵ ![]() 平面
平面 ![]() ,
,
∴ ![]() ,即
,即 ![]() ,解得:
,解得: ![]() ,
,
∴点 ![]() 的坐标为
的坐标为 ![]() ,
,
此时 ![]() ,
,
∴点 ![]() 是线段
是线段 ![]() 靠近
靠近 ![]() 点的三等分点.
点的三等分点.
【解析】(1)证明线面垂直的要点就是在平面内找互两条相交直线都与所证直线垂直。
(2)求二面角时,往往建立空间直角坐标系用两个平面的法向量的夹角来求。
(3)要确定点 M 的位置,使得 AM∥平面BEF,可先设点M的坐标,则向量AM与平面的法向量垂直即可。


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,如果满足:对任意
,如果满足:对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称函数
称函数![]() 的一个上界.已知函数
的一个上界.已知函数![]() ,
, ![]() .
.
(1)若函数![]() 为奇函数,求实数
为奇函数,求实数![]() 的值;
的值;
(2)在第(1)的条件下,求函数![]() 在区间
在区间![]() 上的所有上界构成的集合;
上的所有上界构成的集合;
(3)若函数![]() 在
在![]() 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知非空集合A、B满足以下四个条件:
①A∪B={1,2,3,4,5,6,7};②A∩B=;③A中的元素个数不是A中的元素;④B中的元素个数不是B中的元素.
若集合A含有2个元素,则满足条件的A有个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的左、右焦点分别为
的左、右焦点分别为 ![]() ,椭圆
,椭圆 ![]() 过点
过点 ![]() ,直线
,直线 ![]() 交
交 ![]() 轴于
轴于 ![]() ,且
,且 ![]() ,
, ![]() 为坐标原点.
为坐标原点.
(1)求椭圆 ![]() 的方程;
的方程;
(2)设 ![]() 是椭圆
是椭圆 ![]() 的上顶点,过点
的上顶点,过点 ![]() 分别作直线
分别作直线 ![]() 交椭圆
交椭圆 ![]() 于
于 ![]() 两点,设这两条直线的斜率分别为
两点,设这两条直线的斜率分别为 ![]() ,且
,且 ![]() ,证明:直线
,证明:直线 ![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高三模拟考试的学生中随机抽取60名学生,按其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如下部分频率分布直方图,观察图中的信息,回答下列问题: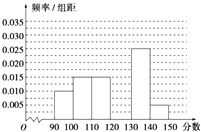
(Ⅰ)补全频率分布直方图;
(Ⅱ)估计本次考试的数学平均成绩(同一组中的数据用该组区间的中点值作代表);
(Ⅲ)用分层抽样的方法在分数段为[110,130)的学生成绩中抽取一个容量为6的样本,再从这6个样本中任取2人成绩,求至多有1人成绩在分数段[120,130)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把一枚质地均匀的骰子投掷两次,记第一次出现的点数为a,第二次出现的点数为b.已知方程组![]()
(1)求方程组只有一个解的概率;
(2)若方程组每个解对应平面直角坐标系中的点P(x,y),求点P落在第四象限的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com