
在某产品的制造过程中,次品率p依赖于日产量x,已知
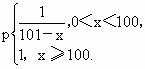
其中x为正整数.又该厂每生产出一件正品可盈利A元,但每产出一件次品就要损失 元,
元,
(1)将该厂的日盈利额T(元)表示为日产量x(个)的函数,并指出这个函数的定义域;
(2)为了获得最大盈利,该厂的日产量应定为多少?
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com