Question

函数f（x）是幂函数，图象过点（2，8），定义在实数R上的函数y=F（x）是奇函数，当x＞0时，F（x）=f（x）+1，求F（x）在R上的表达式；并画出图象．

Answer 1

分析：利用待定系数求出幂函数的表达式，然后根据函数奇偶性的性质求F（x）的表达式即可．

解答：解：设y=x^α，（x＞0）；
将（2，8）代入得α=3，
当x＞0，F（x）=f（x）+1=x³+1，
当x＜0，-x＞0，F（-x）=（-x）³+1=-x³+1，
∵y=F（x）是奇函数，∴F（-X）=-F（X）∴F（x）=x³-1，
∵y=F（x）是定义在实数R上的奇函数，
∴F（0）=0．
∴F(x)=

x3-1，x＜0 0，x=0 x3+1，x＞0

．
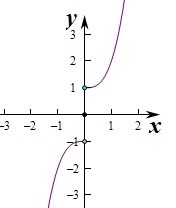
图象见右图：

点评：本题主要考查幂函数的图象和性质，以及函数奇偶性的应用，要求熟练掌握函数性质的综合应用．