
【题目】设函数![]() ,
, ![]() .
.
(Ⅰ)若![]() ,求
,求![]() 的极小值;
的极小值;
(Ⅱ)在(Ⅰ)的条件下,是否存在实常数![]() 和
和![]() ,使得
,使得![]() 和
和![]() ?若存在,求出
?若存在,求出![]() 和
和![]() 的值.若不存在,说明理由;
的值.若不存在,说明理由;
(Ⅲ)设![]() 有两个零点
有两个零点![]() ,且
,且![]() 成等差数列,试探究
成等差数列,试探究![]() 值的符号.
值的符号.
【答案】(1)极小值为0(2)k=2,m= -1(3)![]()
【解析】试题分析:(Ⅰ)首先由![]() ,得到关于
,得到关于![]() 的两个方程,从而求出
的两个方程,从而求出![]() ,这样就可得到
,这样就可得到![]() 的表达式,根据它的特点可想到用导数的方法求出
的表达式,根据它的特点可想到用导数的方法求出![]() 的极小值; (Ⅱ)由(Ⅰ)中所求的
的极小值; (Ⅱ)由(Ⅰ)中所求的![]() 和
和![]() ,易得到它们有一个公共的点
,易得到它们有一个公共的点![]() ,且
,且![]() 和
和![]() 在这个点处有相同的切线
在这个点处有相同的切线![]() ,这样就可将问题转化为证明
,这样就可将问题转化为证明![]() 和
和![]() 分别在这条切线
分别在这条切线![]() 的上方和下方,两线的上下方可转化为函数与0的大小,即证
的上方和下方,两线的上下方可转化为函数与0的大小,即证![]() 和
和![]() 成立,从而得到
成立,从而得到![]() 和
和![]() 的值; (Ⅲ)由已知易得
的值; (Ⅲ)由已知易得![]() ,由零点的意义,可得到关于
,由零点的意义,可得到关于![]() 两个方程,根据结构特征将两式相减,得到关于
两个方程,根据结构特征将两式相减,得到关于![]() 的关系式
的关系式![]() ,又对
,又对![]() 求导,进而得到
求导,进而得到![]() ,结合上面关系可化简得:
,结合上面关系可化简得: 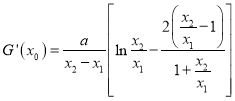 ,针对特征将
,针对特征将![]() 当作一个整体,可转化为关于
当作一个整体,可转化为关于![]() 的函数
的函数![]() ,对其求导分析得,
,对其求导分析得, ![]() 恒成立.
恒成立.
试题解析:解:(Ⅰ)由![]() ,得
,得![]() ,解得
,解得![]() 2分
2分
则![]() =
= ![]() ,
,
利用导数方法可得![]() 的极小值为
的极小值为![]() 5分
5分
(Ⅱ)因![]() 与
与![]() 有一个公共点
有一个公共点![]() ,而函数
,而函数![]() 在点
在点![]() 的切线方程为
的切线方程为![]() ,
,
下面验证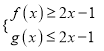 都成立即可 7分
都成立即可 7分
由![]() ,得
,得![]() ,知
,知![]() 恒成立 8分
恒成立 8分
设![]() ,即
,即![]() ,易知其在
,易知其在![]() 上递增,在
上递增,在![]() 上递减,
上递减,
所以![]() 的最大值为
的最大值为![]() ,所以
,所以![]() 恒成立.
恒成立.
故存在这样的k和m,且![]() 10分
10分
(Ⅲ)![]() 的符号为正. 理由为:因为
的符号为正. 理由为:因为![]() 有两个零点
有两个零点![]() ,则有
,则有
![]() ,两式相减得
,两式相减得![]() 12分
12分
即![]() ,于是
,于是![]()
![]()
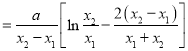
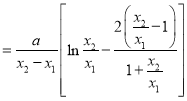 14分
14分
①当![]() 时,令
时,令![]() ,则
,则![]() ,且
,且 .
.
设![]() ,则
,则 ,则
,则![]() 在
在![]() 上为增函数.而
上为增函数.而![]() ,所以
,所以![]() ,即
,即![]() . 又因为
. 又因为![]() ,所以
,所以![]() .
.
②当![]() 时,同理可得:
时,同理可得: ![]() .
.
综上所述: ![]() 的符号为正 16分
的符号为正 16分


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:
【题目】设函数![]() ,
, ![]() .
.
(Ⅰ)若![]() ,求
,求![]() 的极小值;
的极小值;
(Ⅱ)在(Ⅰ)的条件下,是否存在实常数![]() 和
和![]() ,使得
,使得![]() 和
和![]() ?若存在,求出
?若存在,求出![]() 和
和![]() 的值.若不存在,说明理由;
的值.若不存在,说明理由;
(Ⅲ)设![]() 有两个零点
有两个零点![]() ,且
,且![]() 成等差数列,试探究
成等差数列,试探究![]() 值的符号.
值的符号.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“抛阶砖”是国外游乐场的典型游戏之一.参与者只需将手上的“金币”(设“金币”的半径为1)抛向离身边若干距离的阶砖平面上,抛出的“金币”若恰好落在任何一个阶砖(边长为2.1的正方形)的范围内(不与阶砖相连的线重叠),便可获大奖.不少人被高额奖金所吸引,纷纷参与此游戏,但很少有人得到奖品,请用所学的概率知识解释这是为什么.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某校高三年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图.
分组 | 频数 | 频率 |
[10,15) | 10 | 0.25 |
[15,20) | 24 | n |
[20,25) | m | p |
[25,30] | 2 | 0.05 |
合计 | M | 1 |

(1)求出表中M,p及图中a的值;
(2)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间[10,15)内的人数;
(3)估计这次学生参加社区服务人数的众数、中位数以及平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学举行一次“环保知识竞赛”,全校学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为![]() 分)作为样本进行统计,请根据下面尚未完成并有局部污损的样本的频率分布表和频率分布直方图(如图所示)解决下列问题:
分)作为样本进行统计,请根据下面尚未完成并有局部污损的样本的频率分布表和频率分布直方图(如图所示)解决下列问题:
(Ⅰ)写出![]() ,
, ![]() ,
, ![]() ,
, ![]() 的值.
的值.
(Ⅱ)在选取的样本中,从竞赛成绩是![]() 分以上(含
分以上(含![]() 分)的同学中随机抽取
分)的同学中随机抽取![]() 名同学到广场参加环保知识的志愿宣传活动,求所抽取的
名同学到广场参加环保知识的志愿宣传活动,求所抽取的![]() 名同学来自同一组的概率.
名同学来自同一组的概率.
(Ⅲ)在(Ⅱ)的条件下,设![]() 表示所抽取的
表示所抽取的![]() 名同学中来自第
名同学中来自第![]() 组的人数,求
组的人数,求![]() 的分布列及其数学期望.
的分布列及其数学期望.
组别 | 分组 | 频数 | 频率 |
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
合计 |
|
|

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂对一批产品进行了抽样检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106].已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( )
A. 90 B. 75
C. 60 D. 45
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com