练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （08年厦门外国语学校模拟）（12分）

    某人抛掷一枚硬币，出现正反面的概率都是，构造数列，

    使，记

        （1）已知，求前两次均为正面，之后反面的有且只有两次是连续出现的概率。

        （2）出现正面记2分，出现反面记分，此人共抛掷了三次硬币，求得分的数学期望。

    解析：（1）当前两次出现正面时，要使，需后6次3次正面3次反面，其中反面有两次是连续出现的，设其概率为，则………………6分

        （2）用表示得分，分布列为：

    0

    3

    6

         得分的数学期望为：………………12分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：徐汇区二模 题型：填空题

    设函数f（x）=x（
    1
    2
    ）x+
    1
    x+1
    ，O为坐标原点，An为函数y=f（x）图象上横坐标为n（n∈N*）的点，向量
    OAn
    与向量
    i
    =（1，0）的夹角为θn，则满足tanθ1+tanθ2+…+tanθn＜
    5
    3
    的最大整数n的值为______．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    已知数列{an}满足3an+1+an=4（n∈N*）且a1=9，其前n项和为Sn，则满足不等式|Sn-n-6|＜
    1
    125
    的最小正整数n是______．

    查看答案和解析>>

    科目：高中数学 来源：0103 模拟题 题型：解答题

    设对于任意的实数x，y，函数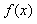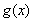，满足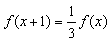， 且f（0）=3，g（x+y）=g（x）+
    2y，g（5）=13，n∈N*。
    （Ⅰ）求数列和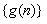的通项公式；
    （Ⅱ）设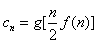，求数列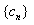的前n项和Sn；
    （Ⅲ）设F（n）=Sn-3n，存在整数m和M，使得对任意正整数n不等式m<F（n）<M恒成立，求M-m的最小值。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    已知数列{an}满足a1=2，an+1=
    an-1
    an
    ，n∈N*    ，则数列{an}的前2013项的和S2013=______．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    一般地，在数列{an}中，如果存在非零常数T，使得am+T=am对任意正整数m均成立，那么就称{an}为周期数列，其中T叫做数列{an}的周期．已知数列{xn}满足xn+1=|xn-xn-1|（n≥2，n∈N*），如果x1=1，x2=a，（a≤1，a≠0），设S2009为其前2009项的和，则当数列{xn}的周期为3时，S2009=______．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    复数z=i+i2+i3+i4+…+i2007+i2008+i2009的值是______．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    设Sn=
    1
    2
    +
    1
    6
    +
    1
    12
    +…+
    1
    n(n+1)
    ， 且 Sn•Sn+1=
    3
    4
    ，则n的值为______．

    查看答案和解析>>

    科目：高中数学 来源：河南模拟 题型：单选题

    设数列{an}是以2为首项，1为公差的等差数列，{bn}是以1为首项，2为公比的等比数列，则ab1+ab2+…+ab10=（　　）
    A．1033B．1034C．2057D．2058

    查看答案和解析>>

    同步练习册答案