
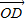 |=1,
|=1,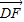 =2
=2 ,∠FDO=
,∠FDO= ,试建立适当的坐标系解决以下问题:
,试建立适当的坐标系解决以下问题:
 ,将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用长轴的表示的函数式即可求得范围,从而解决问题.
,将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用长轴的表示的函数式即可求得范围,从而解决问题.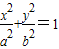 设E(x1,y1),F(x2,y2),
设E(x1,y1),F(x2,y2),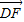 =2
=2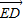 ,知:y1+y2=-y1,且y1y2=-2y12 联立方程组
,知:y1+y2=-y1,且y1y2=-2y12 联立方程组 ,
,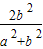 =-y1,y1y2=
=-y1,y1y2=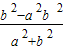 =-2y12,
=-2y12, ∵0<b2<a2,∴0<
∵0<b2<a2,∴0<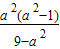 <a2解得:
<a2解得: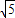 即:椭圆的长轴长的取值范围为(2,2
即:椭圆的长轴长的取值范围为(2,2 ).
).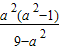 =a2-1,
=a2-1, ,b2=
,b2= ∴椭圆方程为:
∴椭圆方程为: .
.

科目:高中数学 来源: 题型:
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
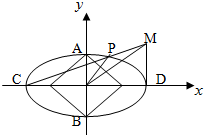 如图,已知椭圆
如图,已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
| OM |
| OP |
查看答案和解析>>
科目:高中数学 来源: 题型:
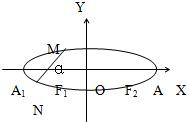
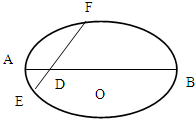 如图,已知椭圆长轴端点A、B,弦EF与AB交于点D,O为中心,且|
如图,已知椭圆长轴端点A、B,弦EF与AB交于点D,O为中心,且|| OD |
| DF |
| ED |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源:1983年全国统一高考数学试卷(理科)(解析版) 题型:解答题
 ,过椭圆焦点F1作一直线,交椭圆于两点M,N,设∠F2F1M=α(0≤α<π)当α取什么值时,|MN|等于椭圆短轴的长?
,过椭圆焦点F1作一直线,交椭圆于两点M,N,设∠F2F1M=α(0≤α<π)当α取什么值时,|MN|等于椭圆短轴的长?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com