
【题目】在△ABC中,AC=3,BC=4,AB=5,以AB所在直线为轴,三角形面旋转一周形成一旋转体,求此旋转体的表面积和体积.
![]()
【答案】表面积为![]() π,体积为
π,体积为![]() π.
π.
【解析】
由已知三角形ABC为直角三角形,斜边AB为轴旋转一周,所得旋转体是AB边的高CO为底面半径的两个圆锥组成的组合体,计算出底面半径及两个圆锥高的和,代入圆锥体积公式,即可求出旋转体的体积;又由该几何体的表面积是两个圆锥的侧面积之和,分别计算出两个圆锥的母线长,代入圆锥侧面积公式,即可得到答案.
过C点作CD⊥AB,垂足为D.△ABC以AB所在直线为轴旋转一周,所得到的旋转体是两个底面重合的圆锥,如图所示,
这两个圆锥高的和为AB=5,
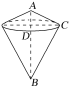
底面半径DC=![]() =
=![]() ,
,
故S表=π·DC·(BC+AC)=![]() π.
π.
V=![]() π·DC2·AD+
π·DC2·AD+![]() π·DC2·BD=
π·DC2·BD=![]() π·DC2(AD+BD)=
π·DC2(AD+BD)=![]() π.
π.
即所得旋转体的表面积为![]() π,体积为
π,体积为![]() π.
π.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知![]() ,且
,且![]() ,函数
,函数![]() ,其中
,其中![]() 为自然对数的底数:
为自然对数的底数:
(1)如果函数![]() 为偶函数,求实数
为偶函数,求实数![]() 的值,并求此时函数的最小值;
的值,并求此时函数的最小值;
(2)对满足![]() ,且
,且![]() 的任意实数
的任意实数![]() ,证明函数
,证明函数![]() 的图像经过唯一的定点;
的图像经过唯一的定点;
(3)如果关于![]() 的方程
的方程![]() 有且只有一个解,求实数
有且只有一个解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
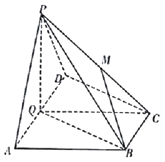
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,平面
,平面![]() 底面
底面![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 是棱
是棱![]() 上的点,
上的点, ![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)若异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 两地相距150千米,某人开汽车以60千米/小时的速度从
两地相距150千米,某人开汽车以60千米/小时的速度从![]() 地到达
地到达![]() 地,在
地,在![]() 地停留1小时后再以50千米/小时的速度返回
地停留1小时后再以50千米/小时的速度返回![]() 地.
地.
(1)试把汽车离开![]() 地的距离
地的距离![]() (千米)表示为时间
(千米)表示为时间![]() (小时)的函数;
(小时)的函数;
(2)根据(1)中的函数表达式,求出汽车距离A地100千米时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
①设某大学的女生体重![]() 与身高
与身高![]() 具有线性相关关系,根据一组样本数据
具有线性相关关系,根据一组样本数据![]() ,用最小二乘法建立的线性回归方程为
,用最小二乘法建立的线性回归方程为![]() ,则若该大学某女生身高增加
,则若该大学某女生身高增加![]() ,则其体重约增加
,则其体重约增加![]() ;
;
②关于![]() 的方程
的方程![]() 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
③过定圆![]() 上一定点
上一定点![]() 作圆的动弦
作圆的动弦![]() ,
,![]() 为原点,若
为原点,若![]() ,则动点
,则动点![]() 的轨迹为椭圆;
的轨迹为椭圆;
④已知![]() 是椭圆
是椭圆![]() 的左焦点,设动点
的左焦点,设动点![]() 在椭圆上,若直线
在椭圆上,若直线![]() 的斜率大于
的斜率大于![]() ,则直线
,则直线![]() (
(![]() 为原点)的斜率的取值范围是
为原点)的斜率的取值范围是![]() .
.
A. ①②③ B. ①③④ C. ①②④ D. ②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中华民族是一个传统文化丰富多彩的民族,各民族有许多优良的传统习俗,如过大年吃饺子,元宵节吃汤圆,端午节吃粽子,中秋节吃月饼等等,让人们感受到浓浓的节目味道,某家庭过大年时包有大小和外观完全相同的肉馅饺子、蛋馅饺子和素馅饺子,一家4口人围坐在桌旁吃年夜饭,当晚该家庭吃饺子时每盘中混放8个饺子,其中肉馅饺子4个,蛋馅饺子和素馅饺子各2个,若在桌上上一盘饺子大家共同吃,记每个人第1次夹起的饺子中肉馅饺子的个数为![]() ,若每个人各上一盘饺子,记4个人中第1次夹起的是肉馅饺子的人数为
,若每个人各上一盘饺子,记4个人中第1次夹起的是肉馅饺子的人数为![]() ,假设每个人都吃饺子,且每人每次都是随机地从盘中夹起饺子.
,假设每个人都吃饺子,且每人每次都是随机地从盘中夹起饺子.
(1)求随机变量![]() 的分布列;
的分布列;
(2)若![]() 的数学期望分别记为
的数学期望分别记为![]() 、
、![]() ,求
,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com