
【题目】以下命题正确的个数是
①函数![]() 在
在![]() 处导数存在,若
处导数存在,若![]() ;
;![]() 是
是![]() 的极值点,则
的极值点,则![]() 是
是![]() 的必要不充分条件
的必要不充分条件
②实数![]() 为实数
为实数![]() ,
,![]() 的等比中项,则
的等比中项,则![]()
③两个非零向量![]() 与
与![]() ,若
,若![]() ,则
,则![]() 与
与![]() 的夹角为钝角
的夹角为钝角
④平面内到一个定点![]() 和一条定直线
和一条定直线![]() 距离相等的点的轨迹叫抛物线
距离相等的点的轨迹叫抛物线
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 高效智能课时作业系列答案
高效智能课时作业系列答案科目:高中数学 来源: 题型:
【题目】如果存在函数![]() (
(![]() 为常数),使得对函数
为常数),使得对函数![]() 定义域内任意
定义域内任意![]() 都有
都有![]() 成立,那么称
成立,那么称![]() 为函数
为函数![]() 的一个“线性覆盖函数”.给出如下四个结论:
的一个“线性覆盖函数”.给出如下四个结论:
①函数![]() 存在“线性覆盖函数”;
存在“线性覆盖函数”;
②对于给定的函数![]() ,其“线性覆盖函数”可能不存在,也可能有无数个;
,其“线性覆盖函数”可能不存在,也可能有无数个;
③![]() 为函数
为函数![]() 的一个“线性覆盖函数”;
的一个“线性覆盖函数”;
④若![]() 为函数
为函数![]() 的一个“线性覆盖函数”,则
的一个“线性覆盖函数”,则![]()
其中所有正确结论的序号是___________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为建立健全国家学生体质健康监测评价机制,激励学生积极参加身体锻炼,教育部印发《国家学生体质健康标准(2014年修订)》,要求各学校每学期开展覆盖本校各年级学生的《标准》测试工作,并根据学生每个学期总分评定等级.某校决定针对高中学生,每学期进行一次体质健康测试,以下是小明同学六个学期体质健康测试的总分情况.
学期 | 1 | 2 | 3 | 4 | 5 | 6 |
总分 | 512 | 518 | 523 | 528 | 534 | 535 |
(1)请根据上表提供的数据,用相关系数![]() 说明
说明![]() 与
与![]() 的线性相关程度,并用最小二乘法求出
的线性相关程度,并用最小二乘法求出![]() 关于
关于![]() 的线性回归方程(线性相关系数保留两位小数);
的线性回归方程(线性相关系数保留两位小数);
(2)在第六个学期测试中学校根据 《标准》,划定540分以上为优秀等级,已知小明所在的学习小组10个同学有6个被评定为优秀,测试后同学们都知道了自己的总分但不知道别人的总分,小明随机的给小组内4个同学打电话询问对方成绩,优秀的同学有![]() 人,求
人,求![]() 的分布列和期望.
的分布列和期望.
参考公式: 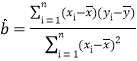 ,
,![]() ;
;
相关系数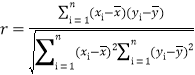 ;
;
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数f(x)=![]() ,其中2<m<2,m∈Z,满足:
,其中2<m<2,m∈Z,满足:
(1)f(x)是区间(0,+∞)上的增函数;
(2)对任意的x∈R,都有f(x) +f(x)=0.
求同时满足条件(1)、(2)的幂函数f(x)的解析式,并求x∈[0,3]时,f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中心在原点,焦点在![]() 轴上的椭圆,下顶点
轴上的椭圆,下顶点![]() ,且离心率
,且离心率![]() .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)经过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() ,
, ![]() 两点.在
两点.在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 恒成立?若存在,求出点
恒成立?若存在,求出点![]() 坐标;若不存在,说明理由.
坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某服装厂生产一种服装,每件服装成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,规定当一次订购量超过100件时,每多订购一件,订购的全部服装的出厂单价就降低![]() 元,根据市场调查,销售商一次订购不会超过600件.
元,根据市场调查,销售商一次订购不会超过600件.
(1)设一次订购![]() 件,服装的实际出厂单价为
件,服装的实际出厂单价为![]() 元,写出函数
元,写出函数![]() 的表达式;
的表达式;
(2)当销售商一次订购多少件服装时,该厂获得的利润最大?其最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的离心率
)的离心率![]() ,左、右焦点分别为
,左、右焦点分别为![]() 、
、![]() ,直线
,直线![]() 过点
过点![]() 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线![]() 垂直
垂直![]() 于点
于点![]() ,线段
,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)当直线![]() 与椭圆
与椭圆![]() 相切,交
相切,交![]() 于点
于点![]() ,
,![]() ,当
,当![]() 时,求
时,求![]() 的直线方程.
的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】运货卡车以每小时x千米的速度匀速行驶130千米,按交通法规限制50≤x≤100(单位:千米/时).假设汽油的价格是每升2元,而汽车每小时耗油![]() 升,司机的工资是每小时14元.
升,司机的工资是每小时14元.
(1)求这次行车总费用y关于x的表达式;
(2)当x为何值时,这次行车的总费用最低,并求出最低费用的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com