
【题目】已知向量 ![]() ,
, ![]() 满足|
满足| ![]() |=2,|
|=2,| ![]() |=1,则下列关系可以成立的而是( )
|=1,则下列关系可以成立的而是( )
A.( ![]() ﹣
﹣ ![]() )⊥
)⊥ ![]()
B.( ![]() ﹣
﹣ ![]() )⊥(
)⊥( ![]() +
+ ![]() )
)
C.( ![]() +
+ ![]() )⊥
)⊥ ![]()
D.( ![]() +
+ ![]() )⊥
)⊥ ![]()
科目:高中数学 来源: 题型:
【题目】函数 ![]() 的最大值为2,它的最小正周期为2π. (Ⅰ)求函数f(x)的解析式;
的最大值为2,它的最小正周期为2π. (Ⅰ)求函数f(x)的解析式;
(Ⅱ)若g(x)=cosxf(x),求g(x)在区间 ![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且2Sn=4an﹣1. (Ⅰ)求{an}的通项公式;
(Ⅱ)设bn=anan+1﹣2,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名篮球运动员在7场比赛中的得分情况如茎叶所示, ![]() 甲、
甲、 ![]() 乙分别表示甲、乙两人的平均得分,则下列判断正确的是( )
乙分别表示甲、乙两人的平均得分,则下列判断正确的是( ) 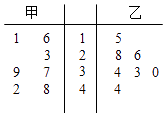
A.![]() 甲>
甲> ![]() 乙 , 甲比乙得分稳定
乙 , 甲比乙得分稳定
B.![]() 甲>
甲> ![]() 乙 , 乙比甲得分稳定
乙 , 乙比甲得分稳定
C.![]() 甲<
甲< ![]() 乙 , 甲比乙得分稳定
乙 , 甲比乙得分稳定
D.![]() 甲<
甲< ![]() 乙 , 乙比甲得分稳定
乙 , 乙比甲得分稳定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的多面体是由一个直平行六面体被平面AEFG所截后得到的,其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°. 
(1)求证:BD⊥平面ADG;
(2)求此多面体的全面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,多面体ABCDE中,AB=AC,平面BCDE⊥平面ABC,BE∥CD,CD⊥BC,BE=1,BC=2,CD=3,M为BC的中点. 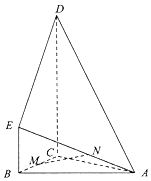
(1)若N是棱AE上的动点,求证:DE⊥MN;
(2)若平面ADE与平面ABC所成锐二面角为60°,求棱AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有10支队伍参加篮球比赛,规定:比赛采取单循环比赛制,即每支队伍与其他9支队伍各比赛一场;每场比赛中,胜方得2分,负方得0分,平局双方各得1分.下面关于这10支队伍得分的叙述正确的是( )
A.可能有两支队伍得分都是18分
B.各支队伍得分总和为180分
C.各支队伍中最高得分不少于10分
D.得偶数分的队伍必有偶数个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在海岸线 ![]() 一侧有一休闲游乐场,游乐场的前一部分边界为曲线段
一侧有一休闲游乐场,游乐场的前一部分边界为曲线段 ![]() ,该曲线段是函数
,该曲线段是函数 ![]() ,
, ![]() 的图像,图像的最高点为
的图像,图像的最高点为 ![]() .边界的中间部分为长1千米的直线段
.边界的中间部分为长1千米的直线段 ![]() ,且
,且 ![]() .游乐场的后一部分边界是以
.游乐场的后一部分边界是以 ![]() 为圆心的一段圆弧
为圆心的一段圆弧 ![]() .
.
(1)求曲线段 ![]() 的函数表达式;
的函数表达式;
(2)曲线段 ![]() 上的入口
上的入口 ![]() 距海岸线
距海岸线 ![]() 最近距离为1千米,现准备从入口
最近距离为1千米,现准备从入口 ![]() 修一条笔直的景观路到
修一条笔直的景观路到 ![]() ,求景观路
,求景观路 ![]() 长;
长;
(3)如图,在扇形 ![]() 区域内建一个平行四边形休闲区
区域内建一个平行四边形休闲区 ![]() ,平行四边形的一边在海岸线
,平行四边形的一边在海岸线 ![]() 上,一边在半径
上,一边在半径 ![]() 上,另外一个顶点P在圆弧
上,另外一个顶点P在圆弧 ![]() 上,且
上,且 ![]() ,求平行四边形休闲区
,求平行四边形休闲区 ![]() 面积的最大值及此时
面积的最大值及此时 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)在R上存在导函数f′(x),对于任意的实数x,都有f(x)=4x2﹣f(﹣x),当x∈(﹣∞,0)时,f′(x)+ ![]() <4x,若f(m+1)≤f(﹣m)+4m+2,则实数m的取值范围是( )
<4x,若f(m+1)≤f(﹣m)+4m+2,则实数m的取值范围是( )
A.[﹣ ![]() ,+∞)
,+∞)
B.[﹣ ![]() ,+∞)
,+∞)
C.[﹣1,+∞)
D.[﹣2,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com