分析:(1)连结AC与BD交于O点,连EO,利用线面垂直的性质与判定证出EO⊥BD,从而点E到面对角线BD的距离即为EO的长,在Rt△EAO中利用勾股定理算出
EO=,即得点E到面对角线BD的距离;
(2)DD
1的中点M,连结AM、FM,证出FM与AB平行且相等,得到四边形FMAB为平行四边形,从而得到平行四边形
AMD
1E中ED
1与AM平行且相等,从而得到四边形EBFD
1是平行四边形,再算出EB=BF即可证出四边形EBFD
1是菱形.
解答:解:(1)连结AC与BD交于O点,连EO,则BD⊥AO
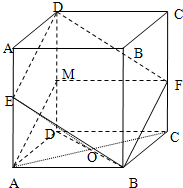
∵EA⊥平面ABCD,∴EO在平面ABCD上的射影为AO
结合BD⊥AO,得EO⊥BD
∴点E到面对角线BD的距离即为EO的长…(3分)
在Rt△EAO中,
EA=,∠EAO=90°,AO=,
∴
EO==即点E到面对角线BD的距离为
…(6分)
(2)取DD
1的中点M,连结AM、FM
∵FM∥CD∥AB,且FM=CD=AB,∴四边形FMAB为平行四边形
可得BF∥AM,且BF=AM
又∵四边形AMD
1E也是平行四边形,
∴ED
1∥AM,且ED
1=AM
∴BF∥ED
1,且BF=ED
1,可得四边形EBFD
1是平行四边形,(10分)
又∵EB=
=BF,∴四边形EBFD
1是菱形…(12分)
点评:本题在正方体中求点线距离,并证明四边形为菱形,着重考查了正方体的性质、线面垂直的判定与性质、勾股定理和平行四边形形的判定与性质等知识,属于中档题.

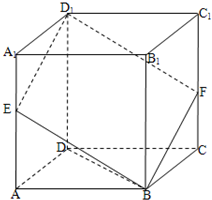 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E、F分别是棱AA1、CC1的中点.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,E、F分别是棱AA1、CC1的中点.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
