
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的方程为
的方程为![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求圆![]() 的极坐标方程与直线
的极坐标方程与直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与圆
与圆![]() 相交于
相交于![]() ,
,![]() 两点,求圆
两点,求圆![]() 在
在![]() ,
,![]() 处两条切线的交点坐标.
处两条切线的交点坐标.
【答案】(1)圆![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的直角坐标方程为
的直角坐标方程为![]() ;(2)
;(2)![]() .
.
【解析】
(1)由题意结合直角坐标方程与极坐标方程的转化公式可得圆![]() 的极坐标方程;转化直线
的极坐标方程;转化直线![]() 的极坐标方程为
的极坐标方程为![]() ,再利用直角坐标方程与极坐标方程的转化公式即可得直线
,再利用直角坐标方程与极坐标方程的转化公式即可得直线![]() 的直角坐标方程;
的直角坐标方程;
(2)由题意联立方程组可得![]() ,
,![]() 的坐标,结合直线与圆相切的性质、直线方程的求解即可得两切线方程,联立方程即可得解.
的坐标,结合直线与圆相切的性质、直线方程的求解即可得两切线方程,联立方程即可得解.
(1)圆![]() 的方程
的方程![]() 可变为
可变为![]() ,
,
所以圆![]() 的极坐标方程为
的极坐标方程为![]() 即
即![]() ;
;
直线![]() 的极坐标方程
的极坐标方程![]() 可变为
可变为![]() ,
,
所以直线![]() 的直角坐标方程为
的直角坐标方程为![]() 即
即![]() ;
;
(2)由题意联立方程组 ,解得
,解得![]() 或
或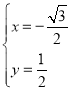 ,
,
不妨设点![]() ,
,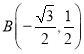 ,设过
,设过![]() ,
,![]() 处的切线分别为
处的切线分别为![]() ,
,![]() ,
,
圆![]() 的圆心为
的圆心为![]() ,半径为
,半径为![]() ,
,
易得![]() ,
,
由直线![]() 的斜率
的斜率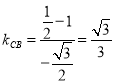 可得直线
可得直线![]() 的斜率
的斜率![]() ,
,
所以直线![]() 的方程为
的方程为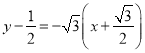 即
即![]() ,
,
由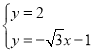 可得
可得 ,
,
所以圆![]() 在
在![]() ,
,![]() 处两条切线的交点坐标为
处两条切线的交点坐标为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前n项和为
的前n项和为![]() ,
,![]()
![]() ,若
,若![]() 是公差不为0的等差数列,且
是公差不为0的等差数列,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)证明:数列![]() 是等差数列;
是等差数列;
(3)记![]() ,若存在
,若存在![]() ,
,![]() (
(![]() ),使得
),使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】稠环芳香烃化合物中有不少是致癌物质,比如学生钟爱的快餐油炸食品中会产生苯并芘,它是由一个苯环和一个芘分子结合而成的稠环芳香烃类化合物,长期食用会致癌.下面是一组稠环芳香烃的结构简式和分子式:
名称 | 萘 | 蒽 | 并四苯 | … | 并n苯 |
结构简式 |
|
|
| … | … |
分子式 |
|
|
| … | … |
由此推断并十苯的分子式为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一款小游戏的规则如下:每轮游戏要进行三次,每次游戏都需要从装有大小相同的2个红球,3个白球的袋中随机摸出2个球,若摸出的“两个都是红球”出现3次获得200分,若摸出“两个都是红球”出现1次或2次获得20分,若摸出“两个都是红球”出现0次则扣除10分(即获得![]() 分).
分).
(1)设每轮游戏中出现“摸出两个都是红球”的次数为![]() ,求
,求![]() 的分布列;
的分布列;
(2)玩过这款游戏的许多人发现,若干轮游戏后,与最初的分数相比,分数没有增加反而减少了,请运用概率统计的相关知识分析解释上述现象.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元五世纪,数学家祖冲之估计圆周率![]() 的值的范围是:
的值的范围是:![]() ,为纪念数学家祖冲之在圆周率研究上的成就,某教师在讲授概率内容时要求学生从小数点后的6位数字1,4,1,5,9,2中随机选取两个数字做为小数点后的前两位(整数部分3不变),那么得到的数字大于3.14的概率为( )
,为纪念数学家祖冲之在圆周率研究上的成就,某教师在讲授概率内容时要求学生从小数点后的6位数字1,4,1,5,9,2中随机选取两个数字做为小数点后的前两位(整数部分3不变),那么得到的数字大于3.14的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,直线
轴的非负半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 与曲线
与曲线![]() 的普通方程;
的普通方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是偶函数,且当
是偶函数,且当![]() 时,
时,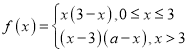
(1)当![]() 时,求
时,求![]() 的解析式;
的解析式;
(2)设函数![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,试求
,试求![]() 的表达式;
的表达式;
(3)若方程![]() 有四个不同的实根,且它们成等差数列,试探求
有四个不同的实根,且它们成等差数列,试探求![]() 与
与![]() 满足的条件.
满足的条件.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com