
【题目】设抛物线 ,点
,点![]()
![]() 在抛物线
在抛物线![]() 上,过焦点
上,过焦点![]() 且斜率为
且斜率为![]() 的直线与
的直线与![]() 相交于
相交于![]() 两点,且
两点,且![]() 两点在准线上的投影分别为
两点在准线上的投影分别为![]() 两点,则三角形
两点,则三角形![]() 的面
的面![]() __________
__________
【答案】![]()
【解析】
先消参得到抛物线C的方程,再将A(1,2)代入抛物线C:y2=2px,解得p,设A(x1,y1),B(x2,y2),利用三角形MFN的面积S△MFN![]() |MN|[1﹣(﹣1)]可得.
|MN|[1﹣(﹣1)]可得.
将抛物线C消去参数t,得到y2=2px,
将A(1,2)代入抛物线C:y2=2px得4=2p,解得p=2,
所以抛物线C的方程为:y2=4x.焦点F(1,0),准线方程为:x=﹣1,
直线AB的方程为:y![]() (x﹣1)代入抛物线C:y2=4x消去x得:y2
(x﹣1)代入抛物线C:y2=4x消去x得:y2![]() y﹣4=0,
y﹣4=0,
设A(x1,y1),B(x2,y2),则y1+y2![]() ,y1y2=﹣4,
,y1y2=﹣4,
∴|MN|=|y1﹣y2|![]() ,
,
∴三角形MFN的面积S△MFN![]() |MN|[1﹣(﹣1)]
|MN|[1﹣(﹣1)]![]() .
.
故答案为![]() .
.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,以
,以![]() ,
,![]() 为邻边作平行四边形
为邻边作平行四边形![]() ,连接
,连接![]() 和
和![]() .
.
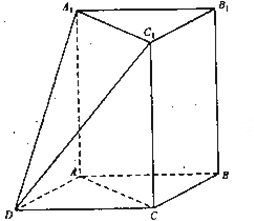
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)线段![]() 上是否存在点
上是否存在点![]() ,使平面
,使平面![]() 与平面
与平面![]() 垂直?若存在,求出
垂直?若存在,求出![]() 的长;若不存在,说明理由.
的长;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科研小组研究发现:一棵水蜜桃树的产量![]() (单位:百千克)与肥料费用
(单位:百千克)与肥料费用![]() (单位:百元)满足如下关系:
(单位:百元)满足如下关系:![]() ,且投入的肥料费用不超过5百元.此外,还需要投入其他成本(如施肥的人工费等)
,且投入的肥料费用不超过5百元.此外,还需要投入其他成本(如施肥的人工费等)![]() 百元.已知这种水蜜桃的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水蜜桃树获得的利润为
百元.已知这种水蜜桃的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水蜜桃树获得的利润为![]() (单位:百元).
(单位:百元).
(1)求利润函数![]() 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;
(2)当投入的肥料费用为多少时,该水蜜桃树获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与椭圆
与椭圆![]() :
:![]() 交于
交于![]() 两点.
两点.
(1)若线段![]() 的中点为
的中点为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)记直线![]() 与
与![]() 轴交于点
轴交于点![]() ,是否存在点
,是否存在点![]() ,使得
,使得![]() 始终为定值?若存在,求点
始终为定值?若存在,求点![]() 的坐标,并求出该定值;若不存在,请说明理由.
的坐标,并求出该定值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人各进行3次投篮,甲每次投中目标的概率为![]() ,乙每次投中目标的概率为
,乙每次投中目标的概率为![]() ,假设两人投篮是否投中相互之间没有影响,每次投篮是否投中相互之间也没有影响。
,假设两人投篮是否投中相互之间没有影响,每次投篮是否投中相互之间也没有影响。
(1)求甲至少有一次未投中目标的概率;
(2)记甲投中目标的次数为![]() ,求
,求![]() 的概率分布及数学期望;
的概率分布及数学期望;
(3)求甲恰好比乙多投中目标2次的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司设计如图所示的环状绿化景观带,该景观带的内圈由两条平行线段(图中的![]() )和两个半圆构成,设
)和两个半圆构成,设![]() ,且
,且![]() .
.
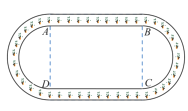
(1)若内圈周长为![]() ,则
,则![]() 取何值时,矩形
取何值时,矩形![]() 的面积最大?
的面积最大?
(2)若景观带的内圈所围成区域的面积为![]() ,则
,则![]() 取何值时,内圈周长最小?
取何值时,内圈周长最小?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com