
已知函数![]() (
(![]() R,且
R,且![]() )的部分图象如图所示.
)的部分图象如图所示.
(1) 求![]() 的值;
的值;
(2) 若方程![]()
在![]() 内有两个不同的解,求实数m的取值范围.
内有两个不同的解,求实数m的取值范围.

解析:(1) 由图象易知函数![]() 的周期为
的周期为![]() (
(![]()
![]()
![]() )=
)=![]() ,∴
,∴![]() .
.
又, ![]() 且
且![]() , 即
, 即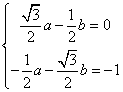 , 解得:
, 解得: ![]() . 所以,
. 所以,
![]()
![]() . [也可以按以下解释: 上述函数的图象可由
. [也可以按以下解释: 上述函数的图象可由![]() 的图象沿
的图象沿![]() 轴负方向平移
轴负方向平移![]() 个单位而得到,∴其解析式为
个单位而得到,∴其解析式为![]() .∴
.∴![]() ]
]
(2)![]() ∴
∴![]() ,∴
,∴![]() .设
.设![]() ,
,
问题等价于方程![]() 在(0,1)仅有一根或有两个相等的根.
在(0,1)仅有一根或有两个相等的根.
方法一:∵- m = 3t2 - t,t Î(0, 1). 作出曲线C:y = 3t2 - t,t Î(0, 1)与直线l:y = - m的图象.
∵t =![]() 时,y =
时,y =![]() ;t = 0时,y = 0;t = 1时,y = 2.
;t = 0时,y = 0;t = 1时,y = 2.
∴当 - m =![]() 或0≤-m<2时,直线l与曲线C有且只有一个公共点.
或0≤-m<2时,直线l与曲线C有且只有一个公共点.
∴m的取值范围是:![]() 或
或![]()
方法二:当 ![]() 仅有一根在(0, 1)时,令
仅有一根在(0, 1)时,令![]() 则
则![]() 得到
得到![]() ; 或
; 或![]() 时
时![]() ,或
,或![]() 时
时![]() (舍去)
(舍去)
当两个等根同在(0,1)内时得到![]() ,
,![]()


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源:2012-2013学年广东省六校高三第 一次联考理科数学试卷(解析版) 题型:解答题
(本小题满分12分)
已知函数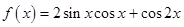 (
(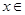 R).
R).
(1) 求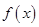 的最小正周期和最大值;
的最小正周期和最大值;
(2) 若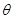 为锐角,且
为锐角,且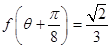 ,求
,求 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com