

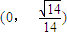 上为增函数,在
上为增函数,在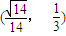 上为减函数,从而得到f(h)的最大值为
上为减函数,从而得到f(h)的最大值为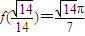 .
.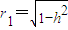 ,
,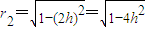 ,
,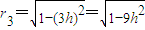 . …(3分)
. …(3分)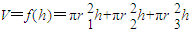
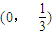 ; …(7分)
; …(7分)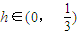 ,
,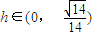 时,f'(h)>0;
时,f'(h)>0;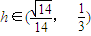 时,f'(h)>0.(11分)
时,f'(h)>0.(11分)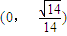 上为增函数,在
上为增函数,在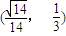 上为减函数,
上为减函数,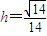 时,f(h)取最大值,这个最大值为
时,f(h)取最大值,这个最大值为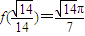 . …(13分)
. …(13分)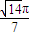 . …(14分)
. …(14分)

 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:
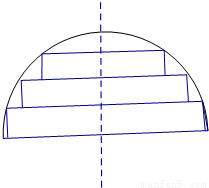
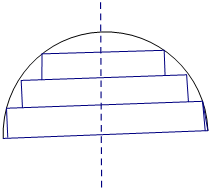 (2012•江苏三模)在一个半径为1的半球材料中截取三个高度均为h的圆柱,其轴截面如图所示,设三个圆柱体积之和为V=f(h).
(2012•江苏三模)在一个半径为1的半球材料中截取三个高度均为h的圆柱,其轴截面如图所示,设三个圆柱体积之和为V=f(h).查看答案和解析>>
科目:高中数学 来源:江苏省苏北四市(徐、淮、连、宿)2012届高三第三次模拟考试数学试题 题型:044
在一个半径为1的半球材料中截取三个高度均为h的圆柱,其轴截面如图所示,设三个圆柱体积之和为V=f(h).
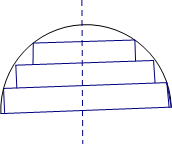
(1)求f(h)的表达式,并写出h的取值范围是;
(2)求三个圆柱体积之和V的最大值;
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省苏北四市高三第三次模拟考试数学试卷(解析版) 题型:解答题
(本小题满分14分)
在一个半径为1的半球材料中截取三个高度均为h的圆柱,其轴截面如图所示,设三个圆柱体积之和为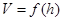 。
。
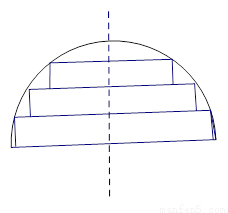
(1) 求f(h)的表达式,并写出h的取值范围是 ;
(2) 求三个圆柱体积之和V的最大值;
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省苏北四市高三第三次质量检测数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com