
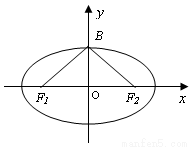
如图,已知椭圆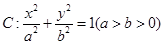 的焦点和上顶点分别为
的焦点和上顶点分别为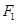 、
、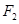 、
、 ,我们称
,我们称 为椭圆
为椭圆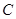 的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.
的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.
(1)已知椭圆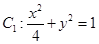 和
和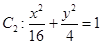 ,判断
,判断 与
与 是否相似,如果相似则求出
是否相似,如果相似则求出 与
与 的相似比,若不相似请说明理由;
的相似比,若不相似请说明理由;
(2)若与椭圆 相似且半短轴长为
相似且半短轴长为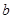 的椭圆为
的椭圆为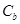 ,且直线
,且直线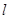 与椭圆为
与椭圆为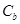 相交于两点
相交于两点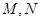 (异于端点),试问:当
(异于端点),试问:当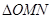 面积最大时,
面积最大时,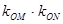 是否与
是否与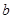 有关?并证明你的结论.
有关?并证明你的结论.
(3)根据与椭圆 相似且半短轴长为
相似且半短轴长为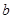 的椭圆
的椭圆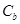 的方程,提出你认为有价值的相似椭圆之间的三种性质(不需证明);
的方程,提出你认为有价值的相似椭圆之间的三种性质(不需证明);
见解析.
【解析】第一问中利用根据已知的的定义进行判定特征三角形是否相似即可
第二问中,设直线方程,借助于联立方程组,和韦达定理可以表示斜率之积,然后可知为定植
第三问中,利用类比推理的思想可知两个相似椭圆之间的性质有:
两个相似椭圆的面积之比为相似比的平方;
分别以两个相似椭圆的顶点为顶点的四边形也相似,相似比即为椭圆的相似比;
两个相似椭圆被同一条直线所截得的线段中点重合;
过原点的直线截相似椭圆所得线段长度之比恰为椭圆的相似比
解:(1)由题意可知,椭圆 的焦点和上顶点分别为
的焦点和上顶点分别为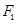 、
、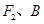 ,我们称
,我们称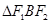 为椭圆C的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比,所以椭圆
为椭圆C的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比,所以椭圆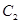 与
与 相似. ………2分
相似. ………2分
因为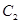 的特征三角形是腰长为4,底边长为
的特征三角形是腰长为4,底边长为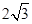 的等腰三角形,
的等腰三角形,
而椭圆 的特征三角形是腰长为2,底边长为
的特征三角形是腰长为2,底边长为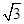 的等腰三角形,
的等腰三角形,
因此两个等腰三角形相似,且相似比为2:1 ……… 4分
(2)椭圆 的方程为:
的方程为: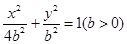 .
.
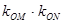 =
= 与b无关
-----------6分
与b无关
-----------6分
(3)椭圆 的方程为:
的方程为: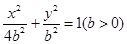 .
.
两个相似椭圆之间的性质有:
两个相似椭圆的面积之比为相似比的平方;
分别以两个相似椭圆的顶点为顶点的四边形也相似,相似比即为椭圆的相似比;
两个相似椭圆被同一条直线所截得的线段中点重合;
过原点的直线截相似椭圆所得线段长度之比恰为椭圆的相似比. ---------------6分


科目:高中数学 来源:2010年北京大学附中高考数学考前猜题试卷(解析版) 题型:解答题
 的焦点和上顶点分别为F1、F2、B,我们称△F1BF2为椭圆C的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.
的焦点和上顶点分别为F1、F2、B,我们称△F1BF2为椭圆C的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比. 和
和 判断C2与C1是否相似,如果相似则求出C2与C1的相似比,若不相似请说明理由;
判断C2与C1是否相似,如果相似则求出C2与C1的相似比,若不相似请说明理由;
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖南省怀化市高三上学期期末考试文科数学试卷(解析版) 题型:解答题
(本小题满分13分)
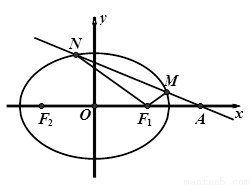
如图,已知椭圆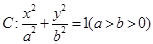 的焦点为
的焦点为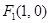 、
、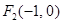 ,离心率为
,离心率为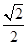 ,过点
,过点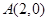 的直线
的直线 交椭圆
交椭圆 于
于 、
、 两点.
两点.
(1)求椭圆 的方程;
的方程;
(2)①求直线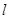 的斜率
的斜率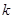 的取值范围;
的取值范围;
②在直线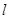 的斜率
的斜率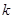 不断变化过程中,探究
不断变化过程中,探究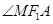 和
和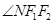 是否总相等?若相等,请给出证明,若不相等,说明理由.
是否总相等?若相等,请给出证明,若不相等,说明理由.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年重庆市高三最后一次模拟考试理数 题型:填空题
如图,已知椭圆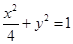 的焦点为
的焦点为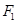 、
、 ,点
,点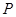 为椭圆上任意一点,过
为椭圆上任意一点,过 作
作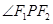 的外角平分线的垂线,垂足为点
的外角平分线的垂线,垂足为点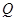 ,过点
,过点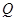 作
作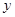 轴的垂线,垂足为
轴的垂线,垂足为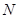 ,线段
,线段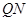 的中点为
的中点为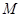 ,则点
,则点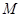 的轨迹方程为________________
的轨迹方程为________________
查看答案和解析>>
科目:高中数学 来源:2010-2011学年四川省成都市高三三诊模拟考试理科数学 题型:填空题
如图,已知椭圆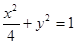 的焦点为F1,F2,点P为椭圆上任意一点,过F2作
的焦点为F1,F2,点P为椭圆上任意一点,过F2作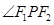 的外角平分线的垂线,垂足为点Q,过点Q作
的外角平分线的垂线,垂足为点Q,过点Q作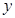 轴的垂线,垂足为N,线段QN的中点为M,则点M的轨迹方程为
。
轴的垂线,垂足为N,线段QN的中点为M,则点M的轨迹方程为
。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com