
| e |
| x |
| 6 |
| y |
| 3 |
| z |
| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:单选题
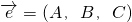 的平面的方程(即平面上任意一点的坐标(x,y,z)满足的关系)是:A(x-x0)+B(y-y0)+C(z-z0)=0”.如果给出平面α的方程是x-y+z=1,平面β的方程是
的平面的方程(即平面上任意一点的坐标(x,y,z)满足的关系)是:A(x-x0)+B(y-y0)+C(z-z0)=0”.如果给出平面α的方程是x-y+z=1,平面β的方程是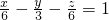 ,则由这两平面所成的二面角的正弦值是
,则由这两平面所成的二面角的正弦值是

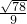

查看答案和解析>>
科目:高中数学 来源: 题型:
(08年龙岩一中冲刺文)我们把平面内与直线垂直的非零向量称为直线的法向量,在平面直线坐标系中,利用求动点轨迹方程的方法,可以求出过点![]() ,且法向量为
,且法向量为![]() 的直线(点法式)方程为
的直线(点法式)方程为![]() ,化简得
,化简得![]() . 类比以上方法,在空间直角坐标系中,经过点
. 类比以上方法,在空间直角坐标系中,经过点![]() 且法向量为
且法向量为![]() 的平面(点法式)方程为_______________________.
的平面(点法式)方程为_______________________.
(请写出化简后的结果)
查看答案和解析>>
科目:高中数学 来源:2011年山东省淄博市周村区高考数学模拟试卷1(解析版) 题型:选择题
 的平面的方程(即平面上任意一点的坐标(x,y,z)满足的关系)是:A(x-x)+B(y-y)+C(z-z)=0”.如果给出平面α的方程是x-y+z=1,平面β的方程是
的平面的方程(即平面上任意一点的坐标(x,y,z)满足的关系)是:A(x-x)+B(y-y)+C(z-z)=0”.如果给出平面α的方程是x-y+z=1,平面β的方程是 ,则由这两平面所成的二面角的正弦值是( )
,则由这两平面所成的二面角的正弦值是( )



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com