
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为矩形,
为矩形, ![]() 平面
平面![]() ,
, ![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 在棱
在棱![]() 上移动.
上移动.
(1)当点![]() 为
为![]() 的中点时,试判断
的中点时,试判断![]() 与平面
与平面![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)求证:无论点![]() 在
在![]() 的何处,都有
的何处,都有![]() ;
;
(3)求二面角![]() 的余弦值.
的余弦值.

【答案】(1)![]() 面
面![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]() .
.
【解析】试题分析:
(1)由于![]() 分别为
分别为![]() 的中点,可得
的中点,可得![]() ,再根据线面平行的判定定理即可证明结果; (2)因为
,再根据线面平行的判定定理即可证明结果; (2)因为![]() 面
面![]() ,可得
,可得![]() ;由于
;由于![]() 为矩形,则
为矩形,则![]() ,根据线面垂直的判定定理,可得
,根据线面垂直的判定定理,可得![]() 面
面![]() ,进而可得
,进而可得![]() .再由于
.再由于![]() ,且
,且![]() 为
为![]() 中点,可得
中点,可得![]() ,于是可证
,于是可证![]() 面
面![]() ,进而求证出结论;(3) 过
,进而求证出结论;(3) 过![]() 作
作![]() 于
于![]() ,
, ![]() 于
于![]() ,连接
,连接![]() ,则
,则![]() 即为所求二面角的平面角.然后再
即为所求二面角的平面角.然后再![]() 中即可求出
中即可求出![]() 的余弦值,即可求出二面角
的余弦值,即可求出二面角![]() 的余弦值.
的余弦值.
试题解析:
(1)∵![]() 分别为
分别为![]() 的中点,
的中点,
∴![]() ,∵
,∵![]() 面
面![]() 面
面![]() ,∴
,∴![]() 面
面![]() .
.
(2)∵![]() 面
面![]() 面
面![]() ,∴
,∴![]() .
.
∵![]() 为矩形,∴
为矩形,∴![]() ,∵
,∵![]() ,∴
,∴![]() 面
面![]() ,
,
∵![]() 面
面![]() ,∴
,∴![]() .
.
∵![]() ,且
,且![]() 为
为![]() 中点,∴
中点,∴![]() .
.
∵![]() ,∴
,∴![]() 面
面![]() ,∵
,∵![]() 面
面![]() ,∴
,∴![]() .
.
(3)
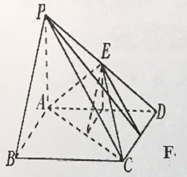
过![]() 作
作![]() 于
于![]() ,
, ![]() 于
于![]() ,连接
,连接![]() ,则
,则![]() 即为所求.易得
即为所求.易得![]() .
.
∵![]() 为矩形,∴
为矩形,∴![]() ,所以点
,所以点![]() 到
到![]() 的距离为
的距离为![]() .
.
∵![]() ,∴
,∴![]() ,∵
,∵![]() 为
为![]() 中点,∴
中点,∴![]() 为
为![]() 中点,
中点,
∴![]() .
.
在![]() 中
中 .
.
∴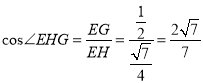 ,
,
即二面角![]() 的余弦值为
的余弦值为![]() .
.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:高中数学 来源: 题型:
【题目】设椭圆中心在坐标原点,A(2,0),B(0,1)是它的两个顶点,直线y=kx(k>0)与AB相交于点D,与椭圆相交于E、F两点.
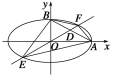
(1)若![]() =6
=6![]() ,求k的值;
,求k的值;
(2)求四边形AEBF面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现从某班的一次期末考试中,随机的抽取了七位同学的数学(满分150分)、物理(满分110分)成绩如下表所示,数学、物理成绩分别用特征量![]() 表示,
表示,
特征量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
t | 101 | 124 | 119 | 106 | 122 | 118 | 115 |
y | 74 | 83 | 87 | 75 | 85 | 87 | 83 |
求![]() 关于t的回归方程;
关于t的回归方程;
(2)利用(1)中的回归方程,分析数学成绩的变化对物理成绩的影响,并估计该班某学生数学成绩130分时,他的物理成绩(精确到个位).
附:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:

![]() .
. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数![]() (m∈Z)为偶函数,且在区间(0,+∞)上是单调增函数.
(m∈Z)为偶函数,且在区间(0,+∞)上是单调增函数.
(1)求函数f(x)的解析式;
(2)设函数![]() ,若g(x)>2对任意的x∈R恒成立,求实数c的取值范围.
,若g(x)>2对任意的x∈R恒成立,求实数c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3-3ax+e,g(x)=1-lnx,其中e为自然对数的底数.
(I)若曲线y=f(x)在点(1,f(1))处的切线与直线l:x+2y=0垂直,求实数a的值;
(II)设函数F(x)=-x[g(x)+![]() x-2],若F(x)在区间(m,m+1)(m∈Z)内存在唯一的极值点,求m的值;
x-2],若F(x)在区间(m,m+1)(m∈Z)内存在唯一的极值点,求m的值;
(III)用max{m,n}表示m,n中的较大者,记函数h(x)=max{f(x),g(x)}(x>0). 若函数h(x)在(0,+∞)上恰有2个零点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】本着健康、低碳的生活理念,租用公共自行车的人越来越多.租用公共自行车的收费标准是每车每次不超过两小时免费,超过两小时的部分每小时2元(不足1小时的部分按1小时计算).甲乙两人相互独立租车(各租一车一次).设甲、乙不超过两小时还车的概率分别为![]() ,
, ![]() ;两小时以上且不超过三小时还车的概率分别为
;两小时以上且不超过三小时还车的概率分别为![]() ,
, ![]() ;两人租车时间都不会超过四小时.
;两人租车时间都不会超过四小时.
(1)求出甲、乙所付租车费用相同的概率;
(2)设甲、乙两人所付的租车费用之和为随机变量![]() ,求随机变量
,求随机变量![]() 的概率分布和期望.
的概率分布和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设P、Q为两个非空集合,定义集合P+Q={m+n| m∈P,n∈Q},若P={0,2,5}, Q={1,2,6},则P+Q中元素的个数为 ( )
A. 9 B. 8 C. 7 D. 6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com