
【题目】已知函数![]() ,
,![]() ,且曲线
,且曲线![]() 与
与![]() 在
在![]() 处有相同的切线.
处有相同的切线.
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)求证:![]() 在
在![]() 上恒成立;
上恒成立;
(Ⅲ)当![]() 时,求方程
时,求方程![]() 在区间
在区间![]() 内实根的个数.
内实根的个数.
【答案】(Ⅰ)![]() ;(Ⅱ)证明见解析;(Ⅲ)2.
;(Ⅱ)证明见解析;(Ⅲ)2.
【解析】
试题分析:
(Ⅰ)函数有相同的切线,则![]() ,
,![]() ,据此计算可得
,据此计算可得![]() ;
;
(Ⅱ)构造函数,令![]() ,原问题等价于
,原问题等价于![]() 在
在![]() 上恒成立,讨论函数的单调性可得
上恒成立,讨论函数的单调性可得![]() ,即
,即![]() 在
在![]() 上恒成立.
上恒成立.
(Ⅲ)构造函数![]() ,其中
,其中![]() ,结合导函数讨论函数的单调性有
,结合导函数讨论函数的单调性有![]()
![]() .构造函数
.构造函数![]() ,则
,则![]() 在
在![]() 内单调递减,
内单调递减,![]() ,据此讨论可得
,据此讨论可得![]() 在区间
在区间![]() 内有两个零点,即方程
内有两个零点,即方程![]() 在区间
在区间![]() 内实根的个数为2.
内实根的个数为2.
试题解析:
(Ⅰ)∵![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,即
,即![]() ,
,
∴![]() .
.
(Ⅱ)证明:设![]() ,
,
![]() .
.
令![]() ,则有
,则有![]() .
.
当![]() 变化时,
变化时,![]() 的变化情况如下表:
的变化情况如下表:

∴![]() ,即
,即![]() 在
在![]() 上恒成立.
上恒成立.
(Ⅲ)设![]() ,其中
,其中![]() ,
,
![]() .
.
令![]() ,则有
,则有![]() .
.
当![]() 变化时,
变化时,![]() 的变化情况如下表:
的变化情况如下表:

∴![]()
![]() .
.
![]() ,
,
设![]() ,其中
,其中![]() ,则
,则![]() ,
,
∴![]() 在
在![]() 内单调递减,
内单调递减,![]() ,
,
∴![]() ,故
,故![]() ,而
,而![]() .
.
结合函数![]() 的图象,可知
的图象,可知![]() 在区间
在区间![]() 内有两个零点,
内有两个零点,
∴方程![]() 在区间
在区间![]() 内实根的个数为2.
内实根的个数为2.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】若对任意![]() ,
, ![]() 有唯一确定的
有唯一确定的![]() 与之对应,则称
与之对应,则称![]() 为关于
为关于![]() ,
, ![]() 的二元函数,现定义满足下列性质的
的二元函数,现定义满足下列性质的![]() 为关于实数
为关于实数![]() ,
, ![]() 的广义“距离”.
的广义“距离”.
(![]() )非负性:
)非负性: ![]() ,当且仅当
,当且仅当![]() 时取等号;
时取等号;
(![]() )对称性:
)对称性: ![]() ;
;
(![]() )三角形不等式:
)三角形不等式: ![]() 对任意的实数
对任意的实数![]() 均成立.
均成立.
给出三个二元函数:①![]() ;②
;②![]() ;③
;③![]() ,
,
则所有能够成为关于![]() ,
, ![]() 的广义“距离”的序号为__________.
的广义“距离”的序号为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称.某市为了了解人们对“一带一路”的认知程度,对不同年龄和不同职业的人举办了一次“一带一路”知识竞赛,满分100分(90分及以上为认知程度高).现从参赛者中抽取了![]() 人,按年龄分成5组,第一组:
人,按年龄分成5组,第一组: ![]() ,第二组:
,第二组: ![]() ,第三组:
,第三组: ![]() ,第四组:
,第四组: ![]() ,第五组:
,第五组: ![]() ,得到如图所示的频率分布直方图,已知第一组有6人.
,得到如图所示的频率分布直方图,已知第一组有6人.
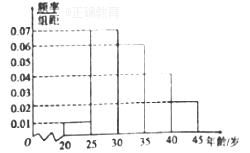
(1)求![]() ;
;
(2)求抽取的![]() 人的年龄的中位数(结果保留整数);
人的年龄的中位数(结果保留整数);
(3)从该市大学生、军人、医务人员、工人、个体户 五种人中用分层抽样的方法依次抽取6人,42人,36人,24人,12人,分别记为1~5组,从这5个按年龄分的组和5个按职业分的组中每组各选派1人参加知识竞赛,分别代表相应组的成绩,年龄组中1~5组的成绩分别为93,96,97,94,90,职业组中1~5组的成绩分别为93,98,94,95,90.
(Ⅰ)分别求5个年龄组和5个职业组成绩的平均数和方差;
(Ⅱ)以上述数据为依据,评价5个年龄组和5个职业组对“一带一路”的认知程度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产甲乙两种产品所得的利润分别为![]() 和
和![]() (万元),它们与投入资金
(万元),它们与投入资金![]() (万元)的关系为:
(万元)的关系为:![]() .今将300万资金投入生产甲乙两种产品,并要求对甲乙两种产品的投入资金都不低于75万元.
.今将300万资金投入生产甲乙两种产品,并要求对甲乙两种产品的投入资金都不低于75万元.
(1)设对乙种产品投入资金![]() (万元),求总利润
(万元),求总利润![]() (万元)关于
(万元)关于![]() 的函数;
的函数;
(2)如何分配投入资金,才能使总利润最大?并求出最大总利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“微信运动”已成为当下热门的健身方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:

(1)若采用样本估计总体的方式,试估计小王的所有微信好友中每日走路步数超过5000步的概率;
(2)已知某人一天的走路步数超过8000步被系统评定“积极型”,否则为“懈怠型”,根据题意完成下面的![]() 列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com