已知数列{an}的奇数项是公差为d1的等差数列,偶数项是公差为d2的等差数列,Sn是数列{an}的前n项和,a1=1,a2=2.
(1)若S5=16,a4=a5,求a10;
(2)已知S15=15a8,且对任意n∈N*,有an<an+1恒成立,求证:数列{an}是等差数列;
(3)若d1=3d2(d1≠0),且存在正整数m、n(m≠n),使得am=an.求当d1最大时,数列{an}的通项公式.
【答案】
分析:(1)确定数列的前5项,利用S
5=16,a
4=a
5,建立方程,求出d
1=2,d
2=3,从而可求a
10;
(2)先证明d
1=d
2,再利用S
15=15a
8,求得d
1=d
2=2,从而可证数列{a
n}是等差数列;
(3)若d
1=3d
2(d
1≠0),且存在正整数m、n(m≠n),使得a
m=a
n,在m,n中必然一个是奇数,一个是偶数.不妨设m为奇数,n为偶数,利用a
m=a
n,及d
1=3d
2,可得
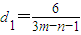
,从而可求当d
1最大时,数列{a
n}的通项公式.
解答:(1)解:根据题意,有a
1=1,a
2=2,a
3=a
1+d
1=1+d
1,a
4=a
2+d
2=2+d
2,a
5=a
3+d
1=1+2d
1
∵S
5=16,a
4=a
5,
∴a
1+a
2+a
3+a
4+a
5=7+3d
1+d
2=16,2+d
2=1+2d
1
∴d
1=2,d
2=3.
∴a
10=2+4d
2=14
(2)证明:当n为偶数时,∵a
n<a
n+1恒成立,∴2+
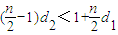
,
∴
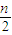
(d
2-d
1)+1-d
2<0
∴d
2-d
1≤0且d
2>1
当n为奇数时,∵a
n<a
n+1恒成立,∴
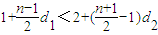
,
∴(1-n)(d
1-d
2)+2>0
∴d
1-d
2≤0
∴d
1=d
2∵S
15=15a
8,∴8+
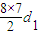
+14+
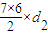
=30+45d
2∴d
1=d
2=2
∴a
n=n
∴数列{a
n}是等差数列;
(3)解:若d
1=3d
2(d
1≠0),且存在正整数m、n(m≠n),使得a
m=a
n,在m,n中必然一个是奇数,一个是偶数
不妨设m为奇数,n为偶数
∵a
m=a
n,∴
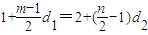
∵d
1=3d
2,∴
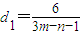
∵m为奇数,n为偶数,∴3m-n-1的最小正值为2,此时d
1=3,d
2=1
∴数列{a
n}的通项公式为a
n=

.
点评:本题考查数列的通项,考查数列的求和,考查学生分析解决问题的能力,确定数列的通项是关键.

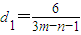 ,从而可求当d1最大时,数列{an}的通项公式.
,从而可求当d1最大时,数列{an}的通项公式.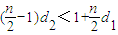 ,
,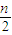 (d2-d1)+1-d2<0
(d2-d1)+1-d2<0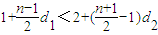 ,
,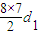 +14+
+14+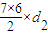 =30+45d2
=30+45d2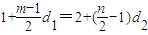
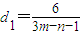
 .
.

 智慧小复习系列答案
智慧小复习系列答案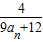 ,求f(0)+f(
,求f(0)+f(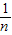 )+f(
)+f(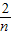 )+…+f(
)+…+f(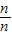 );
);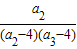 +
+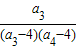 +…+
+…+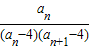 ≥
≥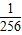 (1-
(1-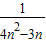 ).
). ,求cn=f(0)+f(
,求cn=f(0)+f( )+f(
)+f( )+…+f(
)+…+f( ),求
),求 +
+ +…+
+…+ 的值.
的值.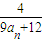 ,求f(0)+f(
,求f(0)+f(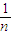 )+f(
)+f(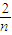 )+…+f(
)+…+f(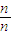 );
);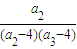 +
+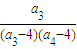 +…+
+…+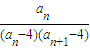 ≥
≥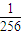 (1-
(1-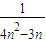 ).
).