【答案】
分析:(Ⅰ)根据题意,有a
1=C
2m+33m•A
m-21,由二项式系数的性质,可得
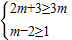
,解可得
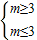
;即m=3,写出
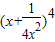
的展开式中的通项的第二项,即可得公比;
(Ⅱ)由(Ⅰ)的结论,可得a
1与公比,可得等比数列的通项为a
n=x
n-1,分x=1与x≠1两种情况讨论,分别求出S
n,综合可得答案;
(Ⅲ)分x=1与x≠1两种情况讨论,当x=1时,S
n=n,A
n=C
n1+2C
n2+3C
n3+…+nC
nn,倒序相加可得2A
n=n(C
n+C
n1+C
n2+…+C
nn),由二项式定理可得2A
n=n•2
n,化简可得A
n=n•2
n-1,当x≠1时,
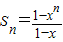
,代入可得A
n的表达式,综合可得答案.
解答:解:(Ⅰ)∵a
1=C
2m+33m•A
m-21∴
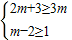
,解可得
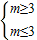
;
∴m=3,
由

的展开式中的通项公式知q=
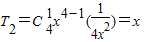
,
(Ⅱ)由(Ⅰ)可得,a
1=C
2m+33m•A
m-21=C
66•A
11=1,其公比为x,
则a
n=x
n-1,
当x=1时,a
n=1,S
n=1+1+…+1=n,
当x≠1时,S
n=
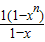
=
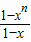
,
则
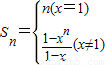
;
(Ⅲ)当x=1时,S
n=n,A
n=C
n1+2C
n2+3C
n3+…+nC
nn=0C
n+C
n1+2C
n2+3C
n3+…+nC
nn①
又∵A
n=nC
nn+(n-1)C
nn-1+(n-2)C
nn-2+…+C
n1+0C
n,②
①+②可得:2A
n=n(C
n+C
n1+C
n2+…+C
nn)=n•2
n,
∴A
n=n•2
n-1,
当x≠1时,
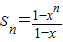
,
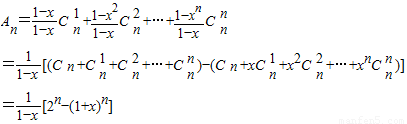
则
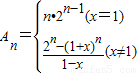
.
点评:本题考查等比数列的求和、二项式定理的应用;注意对等比数列求和时,讨论公比是否为1.

 )4的展开式中的第二项.
)4的展开式中的第二项.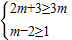 ,解可得
,解可得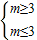 ;即m=3,写出
;即m=3,写出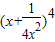 的展开式中的通项的第二项,即可得公比;
的展开式中的通项的第二项,即可得公比;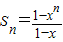 ,代入可得An的表达式,综合可得答案.
,代入可得An的表达式,综合可得答案.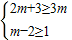 ,解可得
,解可得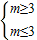 ;
; 的展开式中的通项公式知q=
的展开式中的通项公式知q=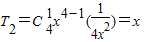 ,
,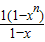 =
=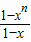 ,
,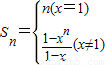 ;
;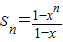 ,
,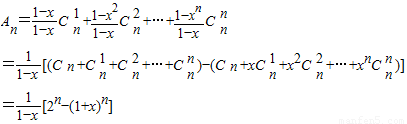
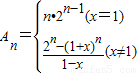 .
.

 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案