
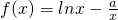 .
. ,求a的值.
,求a的值. .
. ?-a=
?-a= ?a=-
?a=- (与a>0矛盾,舍);
(与a>0矛盾,舍);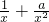 =
=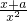 ,
, ,?a=-
,?a=- (舍),
(舍), ?a=-
?a=-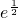 (满足题意),
(满足题意), =
= ,?a=-
,?a=- (舍),
(舍),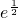 .
. ,解出即可,其最小值分情况进行讨论:当a≥0时据单调性易求最小值;当a<0时,令f′(x)=0得x=
,解出即可,其最小值分情况进行讨论:当a≥0时据单调性易求最小值;当a<0时,令f′(x)=0得x= ,再按照
,再按照 在区间[1,2]外、内两种情况利用单调性即可求得最小值.
在区间[1,2]外、内两种情况利用单调性即可求得最小值.

科目:高中数学 来源:2012-2013学年山东省日照市高三(上)12月段考数学试卷(文科)(解析版) 题型:解答题
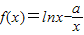 .
. ,求a的值.
,求a的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com