
【题目】已知函数f(x)=x2+2bx,g(x)=|x﹣1|,若对任意x1 , x2∈[0,2],当x1<x2时都有f(x1)﹣f(x2)<g(x1)﹣g(x2),则实数b的最小值为 .
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的部分图象如图所示
)的部分图象如图所示 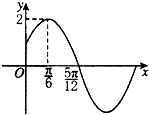
(1)求函数f(x)的解析式;
(2)分析该函数是如何通过y=sinx变换得来的?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2+ax﹣6a2≤0},B={x||x﹣2|<a},
(1)当a=1时,求A∩B和A∪B;
(2)当BA时,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+alnx.
(1)当a=1时,求曲线f(x)在点(1,f(1))处的切线方程;
(2)当a=﹣2时,求函数f(x)的极值;
(3)若函数g(x)=f(x)+ ![]() 在[1,4]上是减函数,求实数a的取值范围.
在[1,4]上是减函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图由图中数据可知身高在[120,130]内的学生人数为( )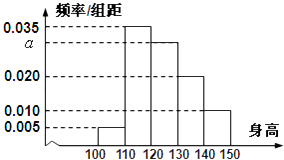
A.20
B.25
C.30
D.35
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,若方程f(x)=a有四个不同的解x1 , x2 , x3 , x4 , 且x1<x2<x3<x4 , 则x3(x1+x2)+
,若方程f(x)=a有四个不同的解x1 , x2 , x3 , x4 , 且x1<x2<x3<x4 , 则x3(x1+x2)+ ![]() 的取值范围是( )
的取值范围是( )
A.(﹣1,+∞)
B.(﹣1,1]
C.(﹣∞,1)
D.[﹣1,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设连续掷两次骰子得到的点数分别为m、n,令平面向量 ![]() ,
, ![]() .
.
(1)求使得事件“ ![]() ”发生的概率;
”发生的概率;
(2)求使得事件“ ![]() ”发生的概率;
”发生的概率;
(3)使得事件“直线 ![]() 与圆(x﹣3)2+y2=1相交”发生的概率.
与圆(x﹣3)2+y2=1相交”发生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com